※본 글에는 수식이 사용되었습니다. 모바일에서는 수식이 깨져 보이지 않을 수 있는 점 참고 바랍니다. 만일 수식이 깨져 보일 경우 데스크톱 모드를 사용하여 주시길 부탁드립니다.
고등학교에서 배우는 이차곡선은 4가지이다. 여기서는 타원에 대해 알아볼 것이다.
타원
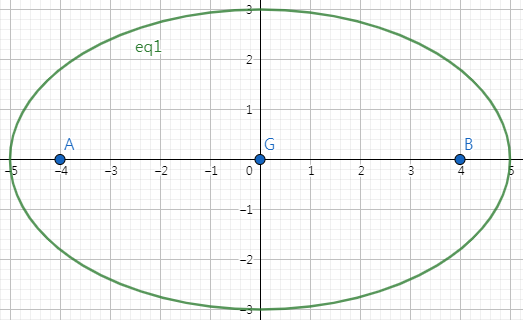
이차곡선 중 타원이라는 도형이 있다. 이 도형은 원과 매우 비슷하게 생겼지만 다른 도형이다. 타원이라는 도형의 정의는 '두 정점으로부터의 거리의 합이 일정한 도형'이다. 여기서 두 정점을 '타원의 초점'이라 하며, 타원의 두 초점의 중점을 '타원의 중심'이라고 한다. 다음의 그림을 보자.


타원의 중심을 지나면서 타원 위의 임의의 두 점을 잇는 선분을 만들어보자. 가장 긴 선분은 타원의 초점을 지나게 되고, 이를 '타원의 장축'이라 한다. 또한 가장 짧은 선분은 장축을 수직이등분하게 되는데, 이를 '타원의 단축'이라고 한다. 타원에서 장축의 절반을 '타원의 긴반지름', 단축의 절반을 '타원의 짧은 반지름'이라고 한다. 타원의 정의에 의하여 두 초점에서 타원 위의 임의의 점까지의 거리의 합은 일정한데, 이 거리의 합은 장축의 길이와 항상 같다.
타원의 방정식
$$ { {x^{2}} \over {a^{2}} } + { {y^{2}} \over {b^{2}} } = 1 \text{ } \left( c^{2} = \left| a^{2}-b^{2} \right| \right) $$
타원은 이차곡선이므로 다른 이차곡선과 같이 x, y에 대한 이차방정식으로 타원의 방정식을 나타낼 수 있다. 다음은 장축이 x축 위에 있는 경우의 타원의 방정식을 유도하는 과정이다.
두 초점 F, F'의 좌표가 각각 (c, 0), (-c, 0)이고, 두 초점에서의 거리의 합이 2a인 타원의 방정식을 유도해보자.
두 초점에서의 거리에 합이 2a가 되도록 하는 점 P의 좌표를 (x, y)라고 두면
$$ \overline{PF} = \sqrt{ \left( x-c \right)^{2}+y^{2} } \text{, } \overline{PF^{\prime}} = \sqrt{ \left( x+c \right)^{2}+y^{2} } $$
$$ \text{이때, } \overline{PF}+\overline{PF^{\prime}} = 2a \text{이므로} $$
$$ \sqrt{ \left( x-c \right)^{2}+y^{2} } +\sqrt{ \left( x+c \right)^{2}+y^{2} } = 2a $$
좌변의 sqrt{ (x+c)^{2}+y^{2} }을 우변으로 이항하면
$$ \sqrt{ \left( x-c \right)^{2}+y^{2} } = 2a-\sqrt{ \left( x+c \right)^{2}+y^{2} } $$
양변을 제곱하면
$$ \left( x-c \right)^{2}+y^{2} = 4a^{2} -4a \sqrt{ \left( x+c \right)^{2}+y^{2} } +\left( x+c \right)^{2}+y^{2} $$
$$ x^{2}-2cx+c^{2} +y^{2} = 4a^{2} -4a \sqrt{ \left( x+c \right)^{2}+y^{2} } + x^{2}+2cx+c^{2} +y^{2} $$
$$ -2cx = 4a^{2} -4a \sqrt{ \left( x+c \right)^{2}+y^{2} } +2cx $$
$$ 4a \sqrt{ \left( x+c \right)^{2}+y^{2} } = 4a^{2} +4cx $$
$$ a \sqrt{ \left( x+c \right)^{2}+y^{2} } = a^{2} +cx $$
양변을 제곱하면
$$ a^{2} \left( \left( x+c \right)^{2}+y^{2} \right) = a^{4} +2a^{2}cx +c^{2}x^{2} $$
$$ a^{2} \left( x^{2}+2cx+c^{2} +y^{2} \right) = a^{4} +2a^{2}cx +c^{2}x^{2} $$
$$ a^{2}x^{2}+2a^{2}cx+a^{2}c^{2} +a^{2}y^{2} = a^{4} +2a^{2}cx +c^{2}x^{2} $$
$$ a^{2}x^{2}+a^{2}c^{2} +a^{2}y^{2} = a^{4} +c^{2}x^{2} $$
상수항은 좌변으로, 상수항이 아닌 항은 우변으로 이항하면
$$ a^{2}x^{2}+a^{2}y^{2} -c^{2}x^{2} = a^{4}-a^{2}c^{2} $$
$$ \left( a^{2}-c^{2} \right)x^{2}+a^{2}y^{2} = a^{2} \left( a^{2}-c^{2} \right) $$
a^{2}-c^{2}=b^{2}으로 두면
$$ b^{2}x^{2}+a^{2}y^{2} = a^{2}b^{2} $$
양변을 a^{2}b^{2}으로 나누면
$$ { {x^{2}} \over {a^{2}} }+{ {y^{2}} \over {b^{2}} } = 1 $$
최종적으로 나온 이 방정식이 타원의 방정식이다. 이 방정식에서 장축의 길이는 2a, 단축의 길이는 2b이다. 장축이 y축 위에 있는 경우 또한 동일한 방법으로 유도할 수 있다. 아래는 장축이 y축 위에 있는 경우의 타원의 방정식을 유도하는 과정이다.
두 초점 F, F'의 좌표가 각각 (0, c), (0, -c)이고, 두 초점에서의 거리의 합이 2b인 타원의 방정식을 유도해보자.
두 초점에서의 거리에 합이 2b가 되도록 하는 점 P의 좌표를 (x, y)라고 두면
$$ \overline{PF} = \sqrt{ \left( y-c \right)^{2}+x^{2} } \text{, } \overline{PF^{\prime}} = \sqrt{ \left( y+c \right)^{2}+x^{2} } $$
$$ \text{이때, } \overline{PF}+\overline{PF^{\prime}} = 2b \text{이므로} $$
$$ \sqrt{ \left( y-c \right)^{2}+x^{2} } +\sqrt{ \left( y+c \right)^{2}+x^{2} } = 2b $$
좌변의 sqrt{ (y+c)^{2}+x^{2} }을 우변으로 이항하면
$$ \sqrt{ \left( y-c \right)^{2}+x^{2} } = 2b-\sqrt{ \left( y+c \right)^{2}+x^{2} } $$
양변을 제곱하면
$$ \left( y-c \right)^{2}+x^{2} = 4b^{2} -4b \sqrt{ \left( y+c \right)^{2}+x^{2} } +\left( y+c \right)^{2}+x^{2} $$
$$ y^{2}-2cy+c^{2} +x^{2} = 4b^{2} -4b \sqrt{ \left( y+c \right)^{2}+x^{2} } + y^{2}+2cy+c^{2} +x^{2} $$
$$ -2cy = 4b^{2} -4b \sqrt{ \left( y+c \right)^{2}+x^{2} } +2cy $$
$$ 4b \sqrt{ \left( y+c \right)^{2}+x^{2} } = 4b^{2} +4bx $$
$$ b \sqrt{ \left( y+c \right)^{2}+x^{2} } = b^{2} +cy $$
양변을 제곱하면
$$ b^{2} \left( \left( y+c \right)^{2}+x^{2} \right) = b^{4} +2b^{2}cy +c^{2}y^{2} $$
$$ b^{2} \left( y^{2}+2cy+c^{2} +x^{2} \right) = b^{4} +2b^{2}cy +c^{2}y^{2} $$
$$ b^{2}y^{2}+2b^{2}cy+b^{2}c^{2} +b^{2}x^{2} = b^{4} +2b^{2}cy +c^{2}y^{2} $$
$$ b^{2}y^{2}+b^{2}c^{2} +b^{2}x^{2} = b^{4} +c^{2}y^{2} $$
상수항은 좌변으로, 상수항이 아닌 항은 우변으로 이항하면
$$ b^{2}y^{2}+b^{2}x^{2} -c^{2}y^{2} = b^{4}-b^{2}c^{2} $$
$$ \left( b^{2}-c^{2} \right)y^{2}+b^{2}x^{2} = b^{2} \left( b^{2}-c^{2} \right) $$
b^{2}-c^{2}=a^{2}으로 두면
$$ b^{2}x^{2}+a^{2}y^{2} = a^{2}b^{2} $$
양변을 a^{2}b^{2}으로 나누면
$$ { {x^{2}} \over {a^{2}} }+{ {y^{2}} \over {b^{2}} } = 1 $$
최종적으로 나온 이 방정식이 타원의 방정식이다. 이 방정식에서 장축의 길이는 2b, 단축의 길이는 2a이다.
타원의 방정식을 보면 여러 정보를 알 수 있다. 항상 장축의 길이는 단축보다 기므로 타원의 방정식을 보면 장축이 어느 축에 평행한지 알 수 있다. 초점의 좌표 역시 알 수 있다.
기하학은 힘이다.
-에우리페데스


