※본 글에는 수식이 사용되었습니다. 모바일에서는 수식이 깨져 보이지 않을 수 있는 점 참고 바랍니다. 만일 수식이 깨져 보일 경우 데스크톱 모드를 사용하여 주시길 부탁드립니다.
앞서 삼각함수를 좌표평면 상에서 원과 직각삼각형으로 정의하였다. 여기에서는 이를 이용하여 삼각항등식에 대해 알아볼 것이다.
삼각항등식의 유도
$$ \sin^{2}{\theta}+\cos^{2}{\theta} = 1 $$
$$ 1+\tan^{2}{\theta} = \sec^{2}{\theta} $$
$$ 1+\cot^{2}{\theta} = \csc^{2}{\theta} $$
이름에서부터 알 수 있듯이 삼각항등식은 삼각함수로 이루어진 항등식이다. 삼각항등식에는 3가지가 있다. 다음 과정을 보며 삼각항등식을 유도해 보자.
$$ \text{유도 - } \sin^{2}{\theta}+\cos^{2}{\theta} = 1 $$
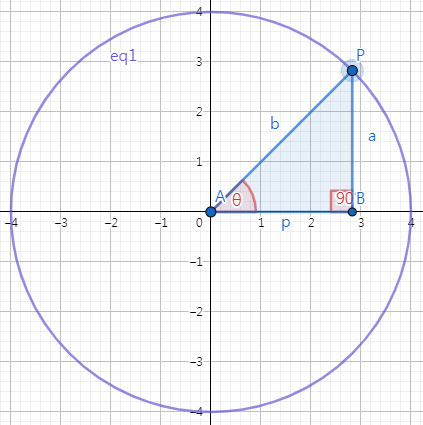
위 그림의 원 eq1의 반지름을 r, 원 eq1 위의 점 P의 좌표를 (x, y)라 하면 다음이 성립한다.
$$ x = r \cos{\theta} \text{, } y = r \sin{\theta} \text{ } \cdots \text{ ⓐ} $$
이때, 원의 방정식은
$$ x^{2}+y^{2} = r^{2} $$
이므로 원의 방정식에 ⓐ를 대입하여 식을 정리하면
$$ r^{2} \cos^{2}{\theta}+r^{2} \sin^{2}{\theta} = r^{2} $$
$$ \sin^{2}{\theta} +\cos^{2}{\theta} = 1 \text{ } \cdots \text{ ①} $$
위의 항등식 ①이 첫번째 삼각항등식이다. 이 항등식은 sin 함수와 cos 함수의 관계를 나타낸다. 나머지 두 삼각항등식은 ①로부터 유도된다.
$$ \text{유도 - } 1+\tan^{2}{\theta} = \sec^{2}{\theta} $$
항등식 ①의 양변을 cos^{2} θ로 나누고 정리하면
$$ { {\sin^{2}{\theta}} \over {\cos^{2}{\theta}} } +1 = { {1} \over {\cos^{2}{\theta}} } $$
$$ 1+\tan^{2}{\theta} = \sec^{2}{\theta} \text{ } \cdots \text{ ②} $$
위의 항등식 ②가 두번째 삼각항등식이다. 이 항등식은 tan 함수와 sec 함수의 관계를 나타낸다.
$$ \text{유도 - } 1+\cot^{2}{\theta} = \csc^{2}{\theta} $$
항등식 ①의 양변을 sin^{2} θ로 나누고 정리하면
$$ 1+{ {\cos^{2}{\theta}} \over {\sin^{2}{\theta}} } = { {1} \over {\sin^{2}{\theta}} } $$
$$ 1+\cot^{2}{\theta} = \csc^{2}{\theta} \text{ } \cdots \text{ ③} $$
위의 항등식 ③이 세번째 삼각항등식이다. 이 항등식은 cot 함수와 csc 함수의 관계를 나타낸다.
위 세 가지 삼각항등식은 치환적분을 하거나 삼각함수의 덧셈정리의 증명 등에서 유용하게 사용된다. 필히 외워두길 권한다.
기하학은 영원히 존재하는 것들에 대한 지식이다.
-플라톤
'수학 > 고등학생을 위한 수학' 카테고리의 다른 글
| 기하와 벡터(2) (0) | 2021.01.20 |
|---|---|
| 기하와 벡터(1) (0) | 2021.01.19 |
| 삼각함수(3) (0) | 2021.01.11 |
| 삼각함수(2) (0) | 2021.01.07 |
| 미분과 적분(43) (0) | 2021.01.06 |


