※본 글에는 수식이 사용되었습니다. 모바일에서는 수식이 깨져 보이지 않을 수 있는 점 참고 바랍니다. 만일 수식이 깨져 보일 경우 데스크톱 모드를 사용하여 주시길 부탁드립니다.
중학교에서 삼각비에 대해 배웠을 것이다. 중학교에서는 sin, cos, tan를 직각삼각형을 통해 정의하고, 특수각에 대해 배우며, 삼각비를 활용하는 방법에 대하여 배운다. 고등학교에서도 크게 다른 점은 없다. 다만 삼각비를 함수화하여 삼각함수로 배우며, 종류가 늘어난다는 차이가 있다. 먼저 고등학교에서 배우는 6가지 삼각비를 보자.
삼각함수
고등학교에서는 6가지 삼각함수를 배운다. 각각 sin1, cos2, tan3, sec4, csc5, cot6이다. 이들 6가지 삼각함수는 하나의 직각삼각형에서부터 정의가 출발한다. 다음 그림을 보며 이들 삼각비를 정의해보자.

위 삼각형은 각 B의 크기가 90º인 직각삼각형이다. 여기서 각 A의 크기를 θ라고 하면 삼각비는 다음과 같이 정의된다.
1. sin
직각삼각형 1에서 sin은 다음과 같이 정의된다.
$$ \sin{\theta} = { {\overline{\mathrm{BC}}} \over {\overline{\mathrm{AC}}} } = { {a} \over {b} } $$

위 그림과 같이 좌표평면 상에 나타낸 직각삼각형 2에서 sin θ를 정의할 수 있다. 좌표평면에 나타난 점 B의 좌표를 (x, y), 원 eq1의 반지름을 r이라고 하면 sin θ는 다음과 같이 정의할 수 있다.
$$ \sin{\theta} = { {y} \over {r} } $$
이 정의에 의하여 각 θ의 동경이 위치하는 사분면에 따라 sin θ의 부호가 결정된다.
$$ \sin{\theta} > 0 \to \text{제 } 1 \text{, } 2 \text{ 사분면} $$
$$ \sin{\theta} < 0 \to \text{제 } 3 \text{, } 4 \text{ 사분면} $$
2. cos
직각삼각형 1에서 cos은 다음과 같이 정의된다.
$$ \cos{\theta} = { {\overline{\mathrm{AB}}} \over {\overline{\mathrm{AC}}} } = { {c} \over {b} } $$

위 그림과 같이 좌표평면 상에 나타낸 직각삼각형 2에서 cos θ를 정의할 수 있다. 좌표평면에 나타난 점 B의 좌표를 (x, y), 원 eq1의 반지름을 r이라고 하면 cos θ는 다음과 같이 정의할 수 있다.
$$ \cos{\theta} = { {x} \over {r} } $$
이 정의에 의하여 각 θ의 동경이 위치하는 사분면에 따라 sin θ의 부호가 결정된다.
$$ \cos{\theta} > 0 \to \text{제 } 1 \text{, } 4 \text{ 사분면} $$
$$ \cos{\theta} < 0 \to \text{제 } 2 \text{, } 3 \text{ 사분면} $$
3. tan
직각삼각형 1에서 tan는 다음과 같이 정의된다.
$$ \tan{\theta} = { {\overline{\mathrm{BC}}} \over {\overline{\mathrm{AB}}} } = { {a} \over {c} } $$
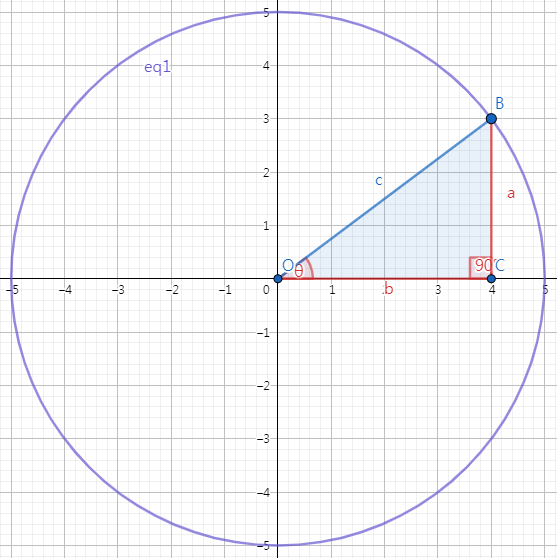
위 그림과 같이 좌표평면 상에 나타낸 직각삼각형 2에서 tan θ를 정의할 수 있다. 좌표평면에 나타난 점 B의 좌표를 (x, y), 원 eq1의 반지름을 r이라고 하면 tan θ는 다음과 같이 정의할 수 있다.
$$ \tan{\theta} = { {y} \over {x} } $$
이 정의에 의하여 각 θ의 동경이 위치하는 사분면에 따라 sin θ의 부호가 결정된다.
$$ \sin{\theta} > 0 \to \text{제 } 1 \text{, } 3 \text{ 사분면} $$
$$ \sin{\theta} < 0 \to \text{제 } 2 \text{, } 4 \text{ 사분면} $$
4. sec
직각삼각형 1에서 sec는 다음과 같이 정의된다.
$$ \sec{\theta} = { {\overline{\mathrm{AC}}} \over {\overline{\mathrm{AB}}} } = { {b} \over {c} } $$
$$ \cos{\theta} = { {\overline{\mathrm{AB}}} \over {\overline{\mathrm{AC}}} } = { {c} \over {b} } $$

위 그림과 같이 좌표평면 상에 나타낸 직각삼각형 2에서 sec θ를 정의할 수 있다. 좌표평면에 나타난 점 B의 좌표를 (x, y), 원 eq1의 반지름을 r이라고 하면 sin θ는 다음과 같이 정의할 수 있다.
$$ \sin{\theta} = { {y} \over {r} } $$
이 정의에 의하여 각 θ의 동경이 위치하는 사분면에 따라 sin θ의 부호가 결정된다.
$$ \sin{\theta} > 0 \to \text{제 } 1 \text{, } 2 \text{ 사분면} $$
$$ \sin{\theta} < 0 \to \text{제 } 3 \text{, } 4 \text{ 사분면} $$
5. csc
직각삼각형 1에서 csc는 다음과 같이 정의된다.
$$ \csc{\theta} = { {\overline{\mathrm{AC}}} \over {\overline{\mathrm{BC}}} } = { {b} \over {a} } $$

위 그림과 같이 좌표평면 상에 나타낸 직각삼각형 2에서 csc θ를 정의할 수 있다. 좌표평면에 나타난 점 B의 좌표를 (x, y), 원 eq1의 반지름을 r이라고 하면 sin θ는 다음과 같이 정의할 수 있다.
$$ \sin{\theta} = { {y} \over {r} } $$
이 정의에 의하여 각 θ의 동경이 위치하는 사분면에 따라 sin θ의 부호가 결정된다.
$$ \sin{\theta} > 0 \to \text{제 } 1 \text{, } 2 \text{ 사분면} $$
$$ \sin{\theta} < 0 \to \text{제 } 3 \text{, } 4 \text{ 사분면} $$
6. cot
직각삼각형 1에서 cot는 다음과 같이 정의된다.
$$ \cot{\theta} = { {\overline{\mathrm{AB}}} \over {\overline{\mathrm{BC}}} } = { {c} \over {a} } $$
$$ \tan{\theta} = { {\overline{\mathrm{BC}}} \over {\overline{\mathrm{AB}}} } = { {a} \over {c} } $$

위 그림과 같이 좌표평면 상에 나타낸 직각삼각형 2에서 cot θ를 정의할 수 있다. 좌표평면에 나타난 점 B의 좌표를 (x, y), 원 eq1의 반지름을 r이라고 하면 sin θ는 다음과 같이 정의할 수 있다.
$$ \sin{\theta} = { {y} \over {r} } $$
이 정의에 의하여 각 θ의 동경이 위치하는 사분면에 따라 sin θ의 부호가 결정된다.
$$ \sin{\theta} > 0 \to \text{제 } 1 \text{, } 2 \text{ 사분면} $$
$$ \sin{\theta} < 0 \to \text{제 } 3 \text{, } 4 \text{ 사분면} $$
정리 - 삼각함수의 성질

삼각함수는 각의 동경이 위치하는 사분면에 따라 부호가 달라진다. 고등학교에서 다루는 삼각함수의 부호를 사분면에 따라 정리해 보자. 동경이 제 1사분면에 위치할 때, 6가지 삼각함수 모두 양수이다. 동경이 제 2사분면에 위치할 때, sin 계열의 삼각함수인 sin과 csc만이 양수이고, 나머지는 음수이다. 동경이 제 3사분면에 위치할 때, tan계열의 삼각함수인 tan와 cot만이 양수이고, 나머지는 음수이다. 동경이 제 4사분면에 위치할 때, cos 계열의 삼각함수인 cos과 sec만이 양수니고, 나머지는 음수이다. 이러한 성질은 삼각함수를 이용할 때7 매우 중요하게 작용한다. 그러므로 얼사탄코 또는 얼사안코 등으로 단어를 만들어 양수가 되는 삼각함수와 사분면 쌍을 외우는 경우가 많다.
순수한 수학자는 과학자라기보다는 오히려 예술가에 가깝다.
-앨런 와츠
'수학 > 고등학생을 위한 수학' 카테고리의 다른 글
| 기하와 벡터(1) (0) | 2021.01.19 |
|---|---|
| 삼각함수(4) (0) | 2021.01.12 |
| 삼각함수(2) (0) | 2021.01.07 |
| 미분과 적분(43) (0) | 2021.01.06 |
| 미분과 적분(42) (0) | 2021.01.05 |

