※본 글에는 수식이 사용되었습니다. 모바일에서는 수식이 깨져 보이지 않을 수 있는 점 참고 바랍니다. 만일 수식이 깨져 보일 경우 데스크톱 모드를 사용하여 주시길 부탁드립니다.
새창으로 열기 - [목차] 원의 성질 - 고등학생을 위한 수학
이전 포스팅에서는 원과 원주각에 대하여 알아보았다. 여기에서는 좌표평면에서 원을 표현하는 방법에 대하여 알아볼 것이다.
과거부터 무언가를 정의하고 표현하는데 힘쓴 사람들이 많이 있었다. 도형 또한 마찬가지로 사람들의 언어와 수학적 용어들을 통해 표현되어 왔다. 처음에는 도형을 그리고 각 도형들의 성질을 이용하여 다른 여러 성질들을 증명하였다. 그러나 이는 각 도형간의 관계를 표현하는데 있어서 불편함이 있었고, 이후 한 철학자가 도형을 표현할 수 있는 새로운 방법을 고안해냈다. 이것이 바로 데카르트가 고안한 좌표평면이다1.
좌표평면
좌표평면은 유클리드 공간 상에서의 위치를 표현하는 좌표계 중 하나로 직교 좌표계 또는 데카르트 좌표계2라고도 부른다3. 자 이렇게 얘기하면 관련된 개념을 알지 못하는 사람은 당연히 뭔 소린지 이해하지 못한다. 여기서 뿐만 아니라 추후 포스팅에서도 2차원 평면 좌표계와 3차원 공간 좌표계를 주로 사용할 것이니 이 둘에만 국한하여 설명하도록 하겠다.
2차원 평면 좌표계는 평평한 무한하게 뻗어있는 평면 상에 수직으로 만나는 두 직선을 축으로, 두 직선의 교점을 원점으로 정의하여 대상을 나타내는 좌표계이다. 3차원 공간 좌표계는 2차원 평면 좌표계의 원점에서 2차원 평면 좌표계와 수직으로 만나는 한 직선을 새로운 축으로 정의하고 대상을 나타내는 좌표계이다. 이러한 방식으로 정의된 좌표평면은 기하를 대수적으로 표현할 수 있게 해 주었다. 다음 글에서 설명할 원의 방정식 또한 원을 대수적으로 표현한 것이다.
원의 방정식
원의 정의를 이용하여 원의 방정식을 유도해 보자.
$$ \text{점 A} \left( a \text{, } b \right) \text{에서 거리가 r인 점 P의 좌표를 } \left( x \text{, } y \right) \text{라고 하면} $$
$$ r = \sqrt{ \left( x-a \right)^{2} + \left( y-b \right)^{2} } \text{이므로} $$
$$ \text{점 P의 자취의 방정식은 다음과 같다.}$$
$$ \left( x-a \right)^{2} + \left( y-b \right)^{2} = r^{2} $$
$$ \therefore \text{원의 중심이 } \left( a \text{, } b \right) \text{이고 반지름이 r인 원의 방정식은} $$
$$ \left( x-a \right)^{2} + \left( y-b \right)^{2} = r^{2} $$
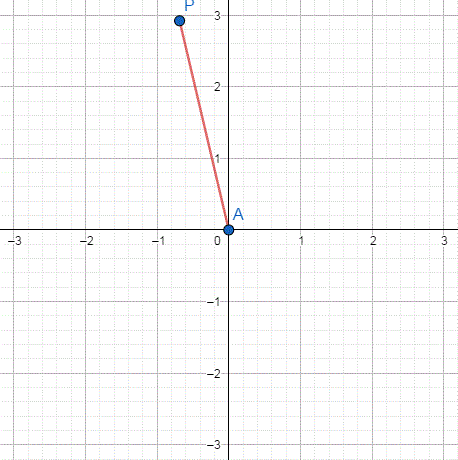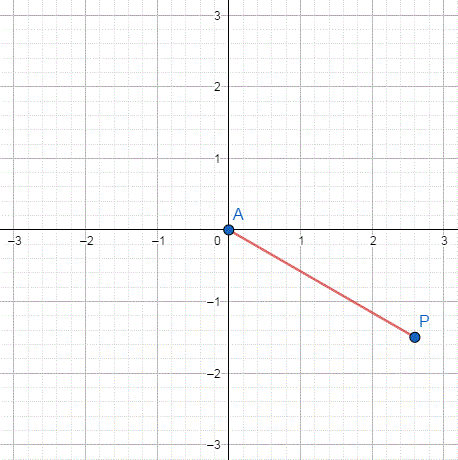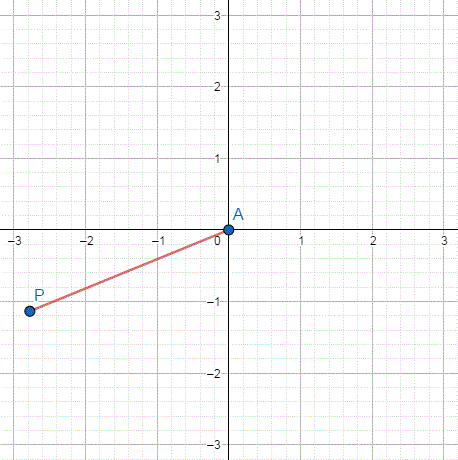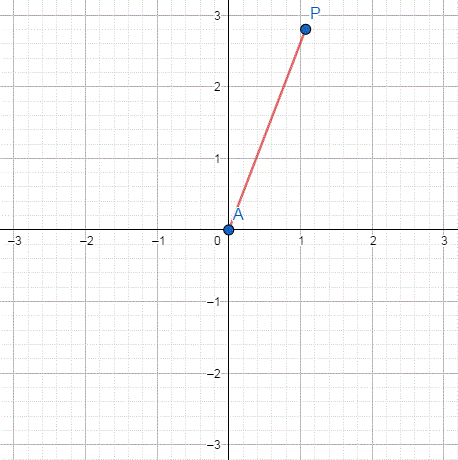
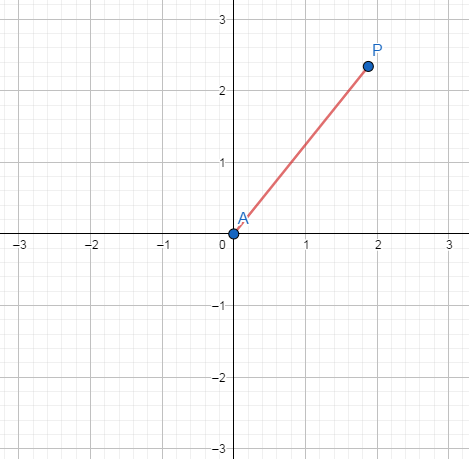
위 그림은 x, y의 값이 변화함에 따라 점 P의 위치 변화를 나타낸 것이다.
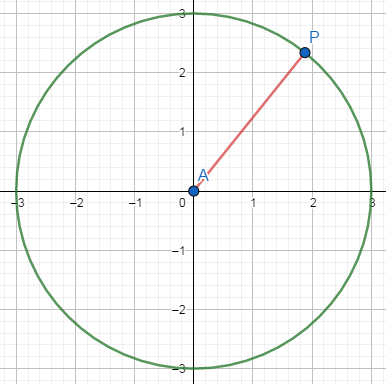
점 P의 자취를 나타내면 위와 같은 원이 나오게 된다. 여기서 점 P의 좌표를 다음과 같이 정의할 수 있다.
$$ \left( r \cos{\theta} \text{, } r \sin{\theta} \right) $$ 4
이렇게 좌표평면을 통해 나타내면 대수적인 표현을 통해 도형을 이해할 수 있게 되어 수식으로 관계 및 정리를 표현함에 있어 편리함을 얻을 수 있다. 필자는 좌표평면 상에서 그래프 등의 도형을 표현하는 능력은 고등학교에서 문제를 해결하는데 매우 중요하다고 생각한다. 특히 수능에서 미적분과 관련된 문제는 대체로 그래프를 잘 그리기만 해도 풀어나갈 방향을 찾는 경우가 허다하다.
나에게는 만물이 수학으로 환원된다.
-데카르트
'수학 > 고등학생을 위한 수학' 카테고리의 다른 글
| 미분과 적분(2) (0) | 2020.10.31 |
|---|---|
| 미분과 적분(1) (0) | 2020.10.27 |
| 원의 성질(1) (0) | 2020.10.24 |
| [공식] 수능에서 도움되는 공식 (0) | 2020.10.20 |
| [서론] 고등학생을 위한 수학 (0) | 2020.10.19 |

