※본 글에는 수식이 사용되었습니다. 모바일에서는 수식이 깨져 보이지 않을 수 있는 점 참고 바랍니다. 만일 수식이 깨져 보일 경우 데스크톱 모드를 사용하여 주시길 부탁드립니다.
수능에서 도움되는 공식은 대체로 내신에서도 도움되므로 밑의 공식들은 가능하면 알아두었으면 한다. 관련 내용은 추후 포스팅할 예정이다.
교과 내
원과 비례

$$\angle{CDP} = \angle{DEP}$$
$$\overline{PA} \times \overline{PB} = \overline{PC} \times \overline{PE}$$
$$\overline{PC} = \overline{PA} = \overline{PB}일때,$$
$$\overline{PD}^{2} = \overline{PC} \times \overline{PE}$$
역함수의 성질
$$ 함수\ y=f(x)에\ 대하여\ g=f^{-1}일때 $$
$$ f(g(x))=x$$
$$ f^{\prime}(g(x))g^{\prime}(x)=1 $$
부분분수
$$ {{1} \over {AB} } = {{1} \over {B-A} } \left( {{1} \over {A} } - {{1} \over {B} } \right) $$
$$ {{a} \over {AB} } = {{a} \over {B-A} } \left( {{1} \over {A} } - {{1} \over {B} } \right) $$
사인 법칙
삼각형 ABC에 대하여 세 변의 길이를 a, b, c, 각 변에 대한 대각을 각각 A, B, C라 할때,
$$ 2R = { { a } \over { \sin{ A } } } = { { b } \over { \sin{ B } } } = { { c } \over { \sin{ C } } } $$
코사인 법칙
삼각형 ABC에 대하여 세 변의 길이를 a, b, c, 각 변에 대한 대각을 각각 A, B, C라 할때,
$$ a^{ 2 } + b^{ 2 } = c^{ 2 } +2ab \cos{ C } $$
$$ b^{ 2 } + c^{ 2 } = a^{ 2 } +2bc \cos{ A } $$
$$ a^{ 2 } + c^{ 2 } = b^{ 2 } +2ac \cos{ B } $$
$$ \cos{ C } = { { a^{ 2 } + b^{ 2 } - c^{ 2 } } \over { 2ab } } $$
$$ \cos{ A } = { { b^{ 2 } + c^{ 2 } - a^{ 2 } } \over { 2bc } } $$
$$ \cos{ B } = { { a^{ 2 } + c^{ 2 } - b^{ 2 } } \over { 2ac } } $$
삼각함수
$$ \sin^{2}{x} + \cos^{2}{x} = 1 $$
$$ 1 + \tan^{2}{x} = \sec^{2}{x} $$
$$ 1 + \cot^{2}{x} = \csc^{2}{x} $$
수열
등차수열
$$ a_{n} = a_{1} + \left( n-1 \right)d \ \left( d \text{는 공차} \right) $$
$$a_{n+1} = a_{n} +d $$
$$ { \sum _{k=1}^{n} { a_{k} } } = { { n \left( a_{1} + a_{n} \right) } \over { 2 } } = { { n \left( 2a_{1} + \left( n-1 \right) d \right) } \over { 2 } } $$
등비수열
$$ a_{n} = a_{1} r^{n-1} \ \left( r \text{은 공비} \right) $$
$$ a_{n+1} = a_{n} r $$
$$ { { a_{n+1} } \over { a_{n} } } = r $$
$$ { \sum _{k=1}^{n} { a_{k} } } = { { a_{1} \left( r^{n}-1 \right) } \over { r-1 } } = { { a_{1} \left( 1-r^{n} \right) } \over { 1-r } } $$
수열의 합
$$ { \sum _{k=1}^{n} { c } } = nc \ \left( c \text{는 상수} \right) $$
$$ { \sum _{k=1}^{n} { k } } = { { n \left( n+1 \right) } \over { 2 } } $$
$$ { \sum _{k=1}^{n} { k^{2} } } = { { n \left( n+1 \right) \left( 2n+1 \right) } \over { 6 } } $$
$$ { \sum _{k=1}^{n} { k^{3} } } = \left( { { n \left( n+1 \right) } \over { 2 } } \right)^{2} $$
미분
$$ \left( x^{p} \right)^{\prime} = \begin{cases} 1 & \left( p=1 \right) \\ px^{p-1} & \left( p \ne 0, p \ne 1 \right) \\ 0 & \left( p=0 \right) \end{cases} \ \left( p \in \Re \right) $$
$$ \left( a^{x} \right)^{\prime} = \begin{cases} e^{x} & \left( a=e \right) \\ a^{x}\ln{a}& \left( a \ne e \right) \end{cases} \ \left( a>0 \right) $$
$$ \left( \log_{a}{x} \right)^{\prime} = \begin{cases} { {1} \over {x} } & \left( a=e \right) \\ { {1} \over { x \ln{a} } } & \left( a \ne e \right) \end{cases} \ \left( a>0 \right) $$
$$ \left( \sin{x} \right)^{\prime} = \cos{x} $$
$$ \left( \cos{x} \right)^{\prime} = -\sin{x} $$
$$ \left( \tan{x} \right)^{\prime} = \sec^{2}{x} $$
$$ \left( \sec{x} \right)^{\prime} = { \sec{x} } { \tan{x} } $$
$$ \left( \csc{x} \right)^{\prime} = -{ \csc{x} } { \cot{x} } $$
$$ \left( \cot{x} \right)^{\prime} = -\csc{x} $$
적분
$$ { \int x^{p}\, dx } = \begin{cases} \ln{ \left| x \right| } +C_{1} & \left( p=-1 \right) \\ { {1} \over {p+1} } x^{p+1} +C_{2} & \left( p \ne -1 \right) \end{cases} \ \left( \text{단, } p \in \Re \text{, } C_{1} \text{, } C_{2} \text{는 적분상수} \right) $$
$$ { \int a^{x}\, dx } = \begin{cases} e^{x} +C_{1} & \left( a=e \right) \\ { { a^{x} } \over { \ln{a} } } +C_{2} & \left( a \ne e \right) \end{cases} \ \left( \text{단, } a>0 \text{, } C_{1} \text{, } C_{2} \text{는 적분상수} \right) $$
$$ { \int ln{x}\, dx } = xln{x} -x +C \ \left( \text{단, } C \text{는 적분상수} \right) $$
$$ { \int \sin{x}\, dx } = -\cos{x} +C \ \left( \text{단, } C \text{는 적분상수} \right) $$
$$ { \int \cos{x}\, dx } = \sin{x} +C \ \left( \text{단, } C \text{는 적분상수} \right) $$
치환적분법
$$ { \int {f^{\prime} \left(g \left(x \right) \right) g^{\prime} \left(x \right)}\, dx } = { \int {f^{\prime} \left(t \right)}\, dt } \ \left( \text{단, } t= g \left(x \right) \right) $$
부분적분법
$$ { \int {f^{\prime} \left(x \right) g \left(x \right)}\, dx } = { f \left(x \right) g \left(x \right) } - { \int {f \left(x \right) g^{\prime} \left(x \right)}\, dx } $$
급수와 정적분의 관계
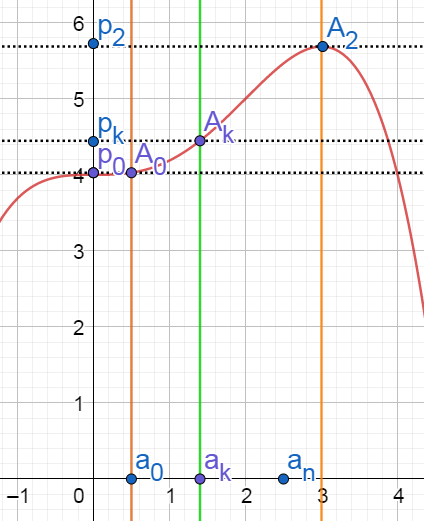
$$ \int^{b}_{a} { f(x) }\, \operatorname{d}\!x = \lim_{n \to \infty} {{ {b-a} \over {n} } \sum_{k=1}^{n} {f \left(a+ {{ \left( b-a \right) k } \over {n}} \right) } } $$
교과 외
로피탈의 정리
$$ \lim_{x \to a} { { { f \left(x \right) } \over { g \left(x \right) } } } = \lim_{x \to a} { { { f^{\prime} \left(x \right) } \over { g^{\prime} \left(x \right) } } } $$ 1
- 이 정리를 만족시키는 두 함수 f(x), g(x)에는 약간의 조건이 붙지만 이는 추후에 다루도록 하겠다. [본문으로]
'수학 > 고등학생을 위한 수학' 카테고리의 다른 글
| 미분과 적분(2) (0) | 2020.10.31 |
|---|---|
| 미분과 적분(1) (0) | 2020.10.27 |
| 원의 성질(2) (0) | 2020.10.25 |
| 원의 성질(1) (0) | 2020.10.24 |
| [서론] 고등학생을 위한 수학 (0) | 2020.10.19 |

