미분과 적분(16)

※본 글에는 수식이 사용되었습니다. 모바일에서는 수식이 깨져 보이지 않을 수 있는 점 참고 바랍니다. 만일 수식이 깨져 보일 경우 데스크톱 모드를 사용하여 주시길 부탁드립니다.

---

 이전에 n차 다항함수의 미분에 대해 다루었다. 이를 통해 n차 다항함수를 미분하였을 때 나타나는 식의 형태를 공식화할 수 있었고, 이는 우리가 도함수를 빠르게 구할 수 있게 해 주었다. 도함수를 통해 우리가 무엇을 알 수 있기에 구하는 것일까?

 도함수는 미분계수를 함수화한 것으로 이해할 수 있다. 바꿔 말해 어떤 지점에서의 순간변화율을 일반화하여 함수로 표현했다고 할 수 있다. 즉 정의역이 변화함에 따라 함수가 어떻게 변화하는지 추정할 수 있게 도와준다. 특히 고등학교에서 배우는 대부분의 함수는 어떤 값에서의 미분계수가 그 지점에서의 접선의 기울기와 값이 같으므로 식만으로는 형태를 알기 힘든 함수의 그래프 또한 도함수를 통해 계형을 알 수 있다. 즉 도함수를 이용하면 함수의 그래프의 계형을 어느 정도 유추 가능하다는 뜻이 된다. 예를 통해 알아보자.

$$ f(x) = x^{3}-x^{2}-5x+3 $$

함수 f(x)의 도함수 f'(x)를 구하면

$$ f^{\prime} = 3x^{2}-2x-5 = (3x-5)(x+1) $$

 이때 도함수 f'(x)가 양수인 구간에서는 함수 f(x)의 함숫값이 증가하고 음수인 구간에서는 감소하므로^[각주:1] 함수 f(x)는 닫힌구간 [-1, 5/3]에서 감소하고 그 외의 구간에서는 증가한다. 함수와 도함수를 이용하면 아래와 같은 표를 만들 수 있다.

$$ x $$	$$ \cdots $$	$$ -1 $$	$$ \cdots $$	$$ { {5} \over {3} } $$	$$ \cdots $$
$$ f^{\prime}(x) $$	$$ + $$	$$ 0 $$	$$ - $$	$$ 0 $$	$$ + $$
$$ f(x) $$	$$ \nearrow $$	$$ 6 $$	$$ \searrow $$	$$ -{ {94} \over {27} } $$	$$ \nearrow $$

이 표가 함수 f(x)의 증가와 감소를 나타낸다고 하여 함수 f(x)의 증감표라고 한다. 증감표는 아래의 방법을 통해 만든다.

1. 도함수 f'(x)를 구한다.
2. 도함수 f'(x)가 0이 되게 하는 c의 값을 구한다.
3. 표의 좌측 칸에 x, f'(x), f(x)를 위에서부터 차례대로 적는다. 이는 차원을 하나씩 올려주는 순서로 적는다고 생각하면 편하다.
4. 표에 x가 적힌 행에는 정의역의 구간을 표시한다. 이를 위해 주어진 구간의 양끝 값과 c의 값을 작은 순서대로 적는다. 이때 각 값의 사이에 빈칸을 두고 ...을 적는다. 또한 주어진 구간의 양끝 값이 둘 중 하나라도 없는 경우에는 없는 위치에 ...만을 적는다. ...과 ...이 연속된다면 둘을 합쳐 ... 하나만을 적어도 된다.
5. 표에 f'(x)가 적힌 행에는 4에서 표시한 구간에서 도함수 f'(x)의 값의 음양과 0을 적는다. 음양의 표현방법은 무엇을 사용하던 상관이 없으나 주로 양수인 구간에서는 +, 음수인 구간에서는 -로 표현한다.
6. 표의 f(x)가 적힌 행에는 4에서 표시한 구간에서 함수 f(x)의 함숫값 또는 함숫값의 변화를 표시한다. 함숫값의 변화는 화살표를 이용한다. 함숫값은 구할 수 있다면 구하면 좋으나 굳이 필요 없을 경우에는 구하지 않아도 된다.

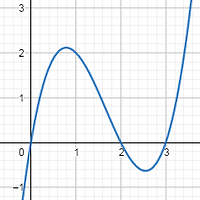
증감표를 이용해 함수 f(x)의 그래프를 그리면 다음과 같이 그릴 수 있다.

 그린 함수의 그래프를 보면 주변보다 상대적으로 크거나 상대적으로 작은 지점, 즉 함수가 증가하다가 감소하거나 감소하다가 증가하는 지점이 존재함을 알 수 있다. 이 지점을 극점이라고 부르고, 극점에서의 함숫값을 극값이라고 부른다. 극값은 다음과 같이 정의할 수 있다.

$$ 구간 X에서 정의된 함수 f(x), 어떤 구간 I \subset X에 대하여 다음을 만족시키는 c \in I가 존재할 때 함숫값 f(c)를 함수 f(x)의 극값이라고 한다. $$
$$ \text{i) } \forall a \in I, \exists c \in I s.t. \in I, f(c) \ge f(a) $$
$$ 이때 x=c에서 함수 f(x)를 극대라고 하고, 함숫값 f(c)를 극댓값이라고 한다. $$
$$ \text{ii) } \forall a \in I, \exists c \in I s.t. f(c) \le f(a) $$
$$ 이때 x=c에서 함수 f(x)를 극소라고 하고, 함숫값 f(c)를 극솟값이라고 한다. $$

이 정의에 의해 함수가 미분 가능하지 않아도 극값을 가질 수 있음을 알 수 있다. 그러나 문제를 풀 때 주로 사용하는 함수는 미분 가능한 함수를 사용하기에 다음의 성질을 사용한다.

$$ \text{미분 가능한 연속함수 } f(x) \text{에 대하여} $$
$$ \text{임의의 열린구간 } (a \text{, } b) \text{에서 도함수 } f^{\prime}(x) \text{가 } f^{\prime}(a)f^{\prime}(b)<0 \text{를 만족하면 } $$
$$ f^{\prime}(c) = 0 \text{인 } c \text{가 적어도 하나 존재한다. 이때 함숫값 } f(c) \text{를 극값이라고 한다.} $$

 즉 도함수가 음양이 바뀌는 지점에서의 함숫값을 극값이라고 한다.

 그래프의 계형을 결정하기 위해 정보가 더 필요할 때, 이계도함수를 활용하여 증감표를 다음과 같은 형태로도 그릴 수 있다.

 함수 f(x)의 이계도함수를 구하면

$$ f^{\prime\prime}(x) = 6x-2 = 2(3x-1) $$

$$ x $$	$$ \cdots $$	$$ -1 $$	$$ \cdots $$	$$ { {1} \over {3} } $$	$$ \cdots $$	$$ { {5} \over {3} } $$	$$ \cdots $$
$$ f^{\prime\prime}(x) $$	$$ - $$	$$ - $$	$$ - $$	$$ 0 $$	$$ + $$	$$ + $$	$$ + $$
$$ f^{\prime}(x) $$	$$ + $$	$$ 0 $$	$$ - $$	$$ - $$	$$ - $$	$$ 0 $$	$$ + $$
$$ f(x) $$		$$ 6 $$		$$ { {34} \over {27} } $$		$$ -{ {94} \over {27} } $$

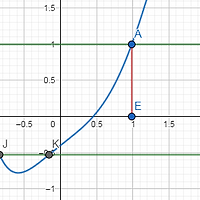
 도함수는 함수의 증가와 감소에 대한 정보를 주며, 이계도함수는 함수의 볼록과 오목에 대한 정보를 준다. 이계도함수가 음수인 구간에서는 함수는 위로 볼록(또는 아래로 오목)하다고 하며, 양수인 구간에서는 아래로 볼록(또는 위로)하다고 한다. 이때 함수의 커브^[각주:2]가 바뀌는 지점을 변곡점이라고 한다.

$$ \text{이계도함수가 존재하는 함수 } f(x) \text{에 대하여} $$
$$ \text{임의의 열린구간 } (a \text{, } b) \text{에서 이계도함수 } f^{\prime\prime}(x) \text{가 } f^{\prime\prime}(a)f^{\prime\prime}(b)<0 \text{를 만족하면 } $$
$$ f^{\prime\prime}(c) = 0 \text{인 } c \text{가 적어도 하나 존재한다. 이때 점 } (c \text{, } f(c)) \text{를 변곡점이라고 한다.} $$

위 그래프에서 볼 수 있듯이 변곡점 C에서 그래프 곡선의 오목과 볼록이 바뀐다.

 변곡점이든 극점이든 주의해야 할 것이 있다. 고등학교에서 나오는 함수의 대부분은 극점과 변곡점을 각각 도함수와 이계도함수가 0이 되는 지점에서 가진다. 그러나 도함수와 이계도함수의 함숫값이 0이라고 해서 항상 극점과 변곡점인 것은 아니며, 심지어 미분계수가 존재하지 않을 때도 극값을 가질 수 있다. 고등학교에서 나오는 함수 중 가끔씩 도함수가 0이 되는 지점은 존재하지만 도함수의 음양이 바뀌지 않아 극값을 가지지 않는 경우가 있다. 이는 주로 삼차 함수나 사 차 함수 같은 차수가 높은 함수에서 빈번하게 보인다. 그러므로 극값이나 변곡점의 좌표를 구할 필요가 있을 경우에는 도함수와 이계도함수의 함숫값의 음양이 바뀌는지 확인하여 실수하지 않고 문제를 해결할 수 있기 바란다.

 

 

 

중/고등학교에서 가르치는 수학은 1800년 이후에 새로 밝혀진 것이 하나도 없다.

-장 디외도네

---

1. 도함수가 양수라는 것은 그 구간에서 접선의 기울기가 양수, 도함수가 음수라는 것은 그 구간에서 접선의 기울기가 음수라고 생각하면 이해하기 편하다. [본문으로]
2. 곡선의 형태 [본문으로]