※본 글에는 수식이 사용되었습니다. 모바일에서는 수식이 깨져 보이지 않을 수 있는 점 참고 바랍니다. 만일 수식이 깨져 보일 경우 데스크톱 모드를 사용하여 주시길 부탁드립니다.
이전에 했어야 하는 주제이나 깜빡하고 빼먹은 내용이 있다. 고등학교 수학 수업에서는 사잇값 정리라고 배우는 중간값 정리이다. 여기서는 중간값 정리에 대해 알아볼 것이다.
중간값 정리는 주어진 구간에서 연속인 함수의 성질 중 하나를 말한다. 중간값 정리는 다음과 같이 서술된다.
$$ \text{연속함수 } f:\left[ a \text{, } b \right] \to R \text{에 대하여} $$
$$ f([a \text{, } b]) \supseteq [f(a) \text{, } f(b)] \cup [f(b) \text{, } f(a)] $$
(구간 [a, b]에서 연속인 함수 f(x)의 구간 [a, b]에서의 치역은 f(a), f(b) 사이의 값을 포함한다.)
$$ \text{연속함수 } f:\left[ a \text{, } b \right] \to R \text{에 대하여} $$
$$ \forall u \in [f(a) \text{, } f(b)] \cup [f(b) \text{, } f(a)] \text{, } \exists c \in [a \text{, } b] \text{ s.t. } f(c) = u $$
(구간 [a, b])에서 연속인 함수 f(x)는 f(a), f(b) 사이의 임의의 값 u에 대하여 f(c)=u인 c가 구간 [a, b]에서 존재한다.)
주어진 구간에서 연속인 함수는 구간의 양끝 값에서의 함숫값 사이의 값을 함숫값으로 가지는 c가 주어진 구간 내에 적어도 하나 존재한다고 풀어 말할 수 있다. 이에 대한 증명은 고등학교에서는 서술하기 힘드므로 예를 통해 이해해 보도록 하자.
먼저 특정 구간에서 연속인 함수를 정의하자.
$$ f(x) = -{{1} \over {2}}x^{5} +x^{4} +{ {1} \over {5} }x^{3} -{ {1} \over {16} }x^{2} +{ {4} \over {5} }x -{ {2} \over {5} } $$
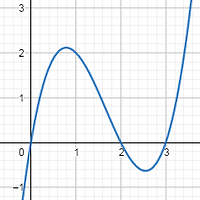
위 그래프에서 보이듯이 주어진 함수 f(x)는 닫힌구간 [E, F]에서 연속이다. 이 구간에서 함수의 치역1은 구간 [f(E), f(F)]2가 되기도 하고, 이 범위보다 커지기도 한다. 여기서 구간 [f(E), f(F)]3 사이의 값을 함숫값으로 가지게 하는 정의역 내의 원소4가 항상 존재함을 알 수 있다.
이 중간값 정리에 의해 다음의 따름 정리가 유도된다.
따름 정리 1 -볼차노 정리
볼차노 정리는 중간값 정리의 특수한 경우5이다. 볼차노 정리는 다음과 같이 서술 가능하다.
$$ \text{연속함수 } f:\left[ a \text{, } b \right] \to R \text{에 대하여} $$
$$ f(a)f(b)<0 \to \exists c \in [a \text{, } b] \text{ s.t. } f(c) = 0 $$
(구간 [a, b])에서 연속인 함수 f(x)는 f(a)f(b)<0이면 f(c)=0인 c가 구간 (a, b)에서 존재한다.)
즉 특정한 구간에서 함숫값의 곱이 음수이면 그 열린구간 내에 적어도 하나의 실근이 존재한다는 뜻이다. 고등학교에서 중간값 정리를 이용하는 문제는 거의 대부분 근의 존재성을 판별하기 위해 사용하기에 이 볼차노 정리를 이용하여 풀이한다.
따름 정리 2 -홀수차 실수 다항식의 근의 존재
홀수차 실수 다항식의 실근은 항상 존재함을 중간값 정리를 통해 보일 수 있다.
$$ \text{자연수 } n \text{에 대하여 } f(x) = a_{2n-1}x^{2n-1}+a_{2n-2}x_{2n-2}+a_{2n-3}x^{2n-3}+\cdots +a_{1}x+a_{0} $$
$$ (a_{2n-1} \text{, } a_{2n-2} \text{, } a_{2n-3} \text{, } \text{, } \cdots \text{, } a_{1} \text{, } a_{0} \in Re)\text{라고 하면}$$
$$ \text{i}) a_{2n-1}>0 \text{일때} $$
$$ \lim_{x \to \infty}{f(x)} = \infty \text{, } \lim_{x \to -\infty}{f(x)} = -\infty \text{,} $$
$$ \text{ii}) a_{2n-1}<0 \text{일때} $$
$$ \lim_{x \to \infty}{f(x)} = -\infty \text{, } \lim_{x \to -\infty}{f(x)} = \infty $$
$$ \text{이므로 중간값 정리에 의하여 함수 } f(x) \text{는 구간 } (-\infty \text{, } \infty) \text{에서 실근을 가진다.} $$
중간값 정리를 사용하는 문제는 주로 합답형 문제6에서 출제된다. 특히 수능에서 출제될 때는 대체로 20번 내지 21번에서 출제되는데, 이 정리를 쓰는 문제가 자주 출제되지 않다 보니 사용하면 쉽게 해결 가능한 것을 오래 끌고 있는 경우를 상당수 보았다. 이 정리는 직관적으로 이해하기 쉽지만 이 점 때문에 문제를 풀이할 때 생각이 안 나는 것 같다. 이 글을 보는 독자들이 이 정리를 사용하는 것 정도는 익숙해졌음 한다.
이 세상의 이치는 수학 지식 없이 알아낼 수가 없다.
-로저 베이컨
'수학 > 고등학생을 위한 수학' 카테고리의 다른 글
| 미분과 적분(16) (0) | 2020.11.22 |
|---|---|
| 미분과 적분(15) (0) | 2020.11.21 |
| 미분과 적분(13) (0) | 2020.11.17 |
| 미분과 적분(12) (0) | 2020.11.15 |
| 미분과 적분(11) (0) | 2020.11.14 |
