※본문에는 수식이 사용되었습니다. 모바일에서는 수식이 깨져 보이지 않을 수 있는 점 참고 바랍니다. 만일 수식이 깨져 보일 경우 데스크톱 모드를 사용하여 주시길 부탁드립니다.
새창으로 열기 - [목차] 원의 성질 - 고등학생을 위한 수학
다른 도형에서도 볼 수 있듯이 도형의 개수가 둘 이상이면 각 도형 사이의 위치 관계를 확인할 수 있다. 본문에서는 xy좌표평면 위에 있는 두 원의 중심과 반지름이 주어졌을 때, 두 원 사이의 위치 관계에 대해 알아볼 것이다.
두 원 사이의 위치 관계
한 평면 위에 두 원이 있을 때, 생길 수 있는 위치 관계는 두 원이 일치하거나, 서로 다른 두 점에서 만나거나, 한 점에서 만나거나, 만나지 않는 경우로 총 4가지 경우가 존재한다. 특히 두 원이 한 점에서 만나는 경우에는 반드시 두 원이 접한다. 그렇다면 두 원 \( O_{1} \), \( O_{2} \)의 중심을 \( \left( x_{1} \text{, } y_{1} \right) \), \( \left( x_{2} \text{, } y_{2} \right) \), 반지름을 \( r_{1} \), \( r_{2} \)라고 주어졌을 때, 위치 관계를 어떻게 파악할 숫 있을까? 두 원의 중심과 반지름이 주어졌으므로 각 원의 방정식을 구한 뒤 교점을 구할 수 있다. 다만 이 경우에는 두 원의 중심 사이의 거리와 두 원의 반지름의 합과 차를 이용하면 더욱 간단하게 위치 관계를 파악할 수 있으므로, 본문에서는 이 방법에 대하여 다룰 것이며, 원의 방정식을 이용하는 방법은 추후 다루도록 할 것이다.
| 두 원의 중심 사이의 거리 \( d \) | 두 원의 반지름의 합 \( A \) | 두 원의 반지름의 차 \( B \) |
| \( d = \sqrt{ \left( x_{1} -x_{2} \right)^{2} +\left( y_{1} -y_{2} \right)^{2} } \) | \( A = r_{1} +r_{2} \) | \( B = \left| r_{1} -r_{2} \right| \) |
두 원이 일치하는 경우
| \( d = B = 0 \) |

두 원이 일치하는 경우는 두 원의 교점이 무수히 많다는 말과도 같다. 두 원이 일단 일치하려면 두 원의 중심이 같은 위치에 있어야 하며, 두 원의 반지름의 크기가 같아야 한다. 즉, \( ( x_{1} \text{, } y_{1} ) = ( x_{2}, y_{2} ) \), \( r_{1} = r_{2} \)이어야 하는데, 이는 다시 말해 두 원의 중심 사이의 거리와 반지름의 차가 모두 0이라는 의미가 된다. 따라서 두 원이 일치하기 위한 조건은 \( \left( d = 0 \right) \land \left( r_{1} = r_{2} \right) \), 즉 \( d = B = 0 \)이다.
두 원이 서로 다른 두 점에서 만나는 경우
| \( B < d < A \) |
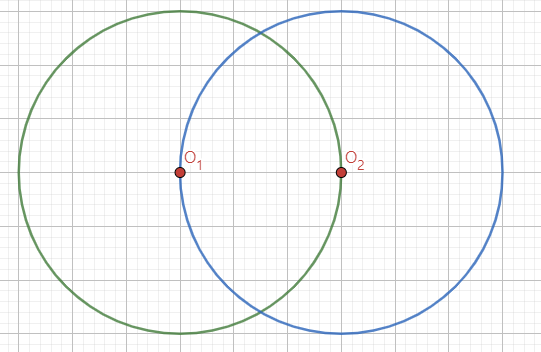
두 원이 서로 다른 두점에서 만나기 위해서는 위의 그림과 같이 두 원의 중심 사이의 거리가 두 반지름의 길이의 합보다 작아야 한다. 즉, \( d < A \)이다. 또한 두 중심 사이의 거리가 두 반지름의 차보다 작으면 한 원이 다른 원의 내부로 들어가게 되므로 두 중심 사이의 거리는 두 반지름의 차보다 커야 한다.1 따라서 두 원이 서로 다른 두 점에서 만나도록 하는 조건은 \( B < d < A \)이다.
두 원이 한 점에서 만나는 경우(접하는 경우)
| \( \left( d = A \right) \lor \left( \left( d = B \right) \land \left( d \ne 0 \right) \right) \) |


두 원이 한 점에서 만나는 경우에는 위의 경우2와 달리 평면 위에 두 원의 위치를 한 원의 내부에서 두 원이 만나느냐, 두 원의 외부에서 두 원이 만나느냐로 두 가지 그릴 수 있다. 먼저 두 원의 외부에서 두 원이 한 점에서 만나는 경우를 보자. 두 원이 한 점에서 만나면 두 원은 접하게 되므로 두 원의 중심 사이의 거리 \( d \)는 두 원의 반지름의 합 \( A \)가 된다. 그러므로 \( d = A \)이면 두 원은 한 점에서 만난다.
다음은 한 원의 내부에서 두 원이 만나는 경우이다. 이 경우에도 역시 두 원은 접하게 되므로 두 원의 중심 사이의 거리 \( d \)는 두 원의 반지름의 차 \( B \)가 된다. 이때, 두 원의 반지름의 차가 0, 다시 말해 중심 사이의 거리가 0이면 두 원이 일치하게 되므로 \( d \ne 0 \)이다. 그러므로 \( \left( d = B \right) \land \left( d \ne 0 \right) \)이다. 따라서 두 경우를 모두 합치면 두 원이 서로 접하는 경우의 조건은 \( \left( d = A \right) \lor \left( \left( d = B \right) \land \left( d \ne 0 \right) \right) \)이다.
두 원이 만나지 않는 경우
| \( \left( d > A \right) \lor \left( d < B \right) \) |



이 경우 역시 위의 경우3처럼 평면 위에 그릴 수 있는 그림의 개수가 여러 개이다. 먼저 중앙의 그림을 보면 두 원의 중심이 일치하고, 두 반지름의 크기가 다름을 알 수 있다. 두 반지름의 크기가 다르면 두 반지름의 차는 양수이다. 그러므로 이 경우를 만족시키는 조건은 \( \left( d = 0 \right) \land \left( B > 0 \right) \)이다.
다음으로 우측의 그림을 보면 두 원의 중심 사이의 거리와 작은 원의 반지름의 길이를 더한 값은 큰 원의 반지름의 길이보다 작다. 그러므로 두 원의 중심 사이의 거리는 항상 두 반지름의 길이의 차보다 작다. 따라서 이 경우를 만족시키는 조건은 \( d < B \)이다. 또한 이 경우는 위의 경우인 \( \left( d = 0 \right) \land \left( B > 0 \right) \)를 포함한다.
마지막으로 좌측의 그림을 보면 두 원의 중심 사이의 거리는 두 반지름의 길이의 합보다 작다. 그러므로 이를 만족시키는 조건은 \( d > A \)이다. 따라서 이 세 가지 경우를 합치면 두 원이 만나지 않는 경우의 조건은 \( \left( d > A \right) \lor \left( d < B \right) \)이다.
내가 푼 문제마다 이후 다른 문제를 푸는데 도움이 되는 규칙이 되었다.
-데카르트
'수학 > 고등학생을 위한 수학' 카테고리의 다른 글
| 집합과 명제(22) (0) | 2021.06.11 |
|---|---|
| 집합과 명제(21) (0) | 2021.06.09 |
| 대수(10) (0) | 2021.06.06 |
| 집합과 명제(20) (0) | 2021.06.04 |
| 집합과 명제(19) (0) | 2021.06.03 |
