※본문에는 수식이 사용되었습니다. 모바일에서는 수식이 깨져 보이지 않을 수 있는 점 참고 바랍니다. 만일 수식이 깨져 보일 경우 데스크톱 모드를 사용하여 주시길 부탁드립니다.
이전 글1에서 여집합과 차집합에 대해 알아보았다. 본문에서는 여집합과 차집합이 가지는 성질에 대해 알아볼 것이다.
여집합과 차집합이 가지는 성질
| 전체집합 U의 두 부분집합 A, B에 대하여 ① \( U^{c} = \varnothing \), \( \varnothing^{c} = U \) ② \( \left( A^{c} \right)^{c} = A \) ③ \( A \cup A^{c} = U \), \( A \cap A^{c} = \varnothing \) ④ \( A-B = A \cap B^{c} \) ⑤ \( A^{c} = U-A \) |
① \( U^{c} = \varnothing \), \( \varnothing^{c} = U \)
전체집합의 여집합은 공집합이 되며, 공집합의 여집합은 전체집합이 된다는 의미이다. 너무나 당연한 소리다.
② \( \left( A^{c} \right)^{c} = A \)
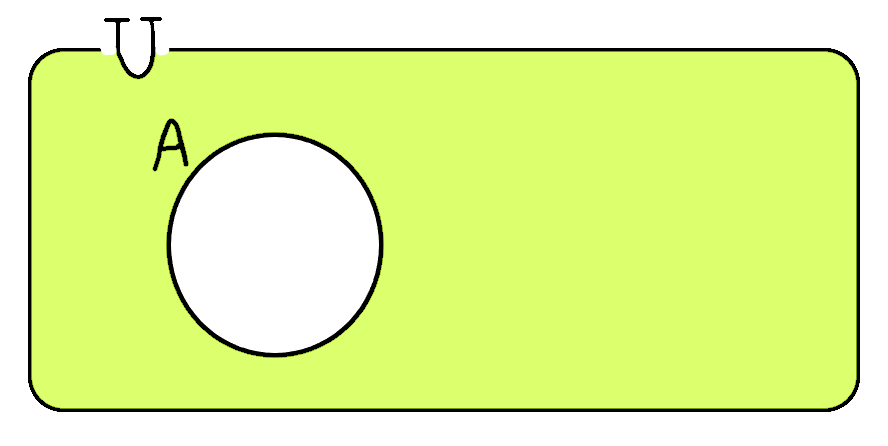
어떤 집합에 여집합 연산을 두 번 수행하면 결과값으로 다시 본래의 집합이 나온다.
③ \( A \cup A^{c} = U \), \( A \cap A^{c} = \varnothing \)

어떤 집합과 그 집합의 여집합에 합집합 연산을 수행하면 전체집합이, 교집합 연산을 수행하면 공집합이 도출된다.
④ \( A-B = A \cap B^{c} \)

두 집합 간의 차집합 연산은 다른 연산을 이용해 표현할 수 있다. 같은 의미의 다른 표현은 아래의 표에 나와 있다.
| \( A-B \) | \( A \cap B^{c} \) | \( A-\left( A \cap B \right) \) | \( \left( A \cup B \right) \) -B | \( B^{c} -A^{c} \) |
⑤ \( A^{c} = U-A \)

이 성질은 여집합 연산을 차집합 연산으로 바꿔 표현할 수 있다는 의미이다.
집합의 연산을 이용한 표현
두 집합 사이의 포함관계
두 집합의 포함관계는 흔히 \( A \subset B \)로 나타낸다. 그러나 이를 집합의 연산을 이용하여 다양하게 나타낼 수 있다. 아래의 표의 모든 내용은 집합 \( A \)가 집합 \( B \)에 속해있음을 나타낸다.
| \( A \subset B \) | ||
| \( A \cap B = A \) | \( A \cup B = B \) | \( A-B = \varnothing \) |
| \( A \cap B^{c} = \varnothing \) | \( B^{c} -A^{c} = \varnothing \) | \( B^{c} \subset A^{c} \) |
서로소인 두 집합
두 집합이 서로소임을 나타내기 위해 흔히 두 집합의 교집합은 공집합임을 나타낸다. 이를 집합의 연산을 이용하여 다양하게 나타낼 수 있다. 아래의 표의 내용은 모두 집합 \( A \)와 집합 \( B \)는 서로소임을 나타낸다.
| \( A \cap B = \varnothing \) | |||
| \( A-B = A \) | \( B-A = B \) | \( A \subset B^{c} \) | \( B \subset A^{c} \) |
여기서 다룬 두 가지 관계 이외에도 집합의 연산을 이용하여 다양한 관계를 표현할 수 있다. 집합 사이의 여러 관계를 독자들이 직접 집합의 연산을 이용하여 표현해보기 바란다.
수학적 진리의 거대한 성은 의심 많은 회의론자들의 공격에도 끄떡없고 흔들리지 않는다.
-버트란드 러셀
'수학 > 고등학생을 위한 수학' 카테고리의 다른 글
| 집합과 명제(15) (0) | 2021.05.28 |
|---|---|
| 집합과 명제(14) (0) | 2021.05.27 |
| 집합과 명제(12) (0) | 2021.05.25 |
| 집합과 명제(11) (0) | 2021.05.24 |
| 대수(7) (0) | 2021.05.23 |



