※본문에는 수식이 사용되었습니다. 모바일에서는 수식이 깨져 보이지 않을 수 있는 점 참고 바랍니다. 만일 수식이 깨져 보일 경우 데스크톱 모드를 사용하여 주시길 부탁드립니다.
합집합과 교집합 연산에 대하여 세 가지 연산법칙이 성립한다. 바로 교환법칙, 결합법칙, 분배법칙이다.
교환법칙
두 집합 \( A \), \( B \)에 대하여 \( A \cup B = B \cup A \), \( A \cap B = B \cap A \)이다. 아래 그림은 벤다이어그램을 통해 교환법칙을 나타낸 그림이다.


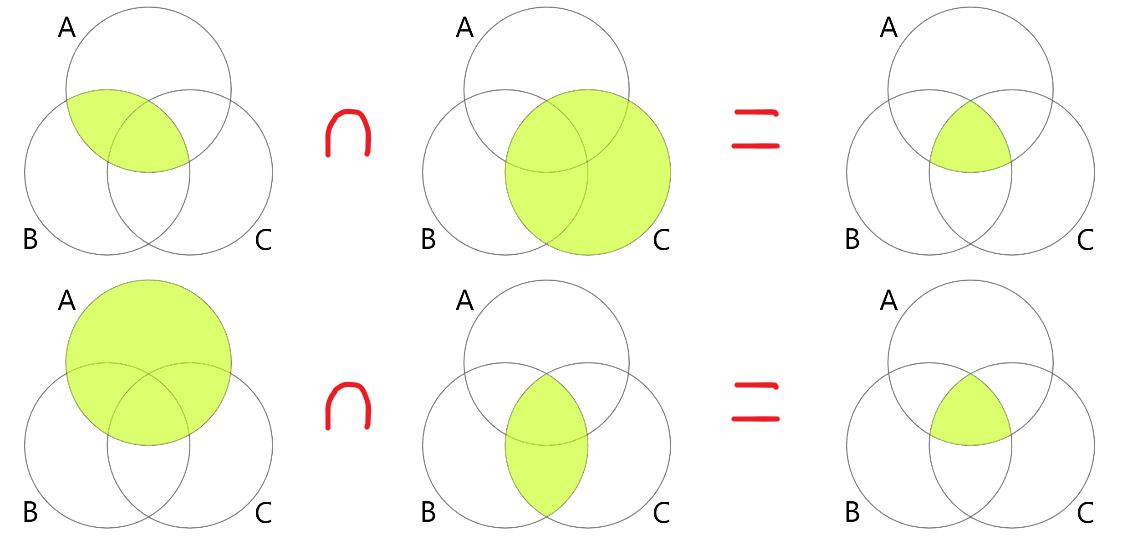
결합법칙
세 집합 \( A \), \( B \), \( C \)에 대하여 \( \left( A \cup B \right) \cup C = A \cup \left( B \cup C \right) \), \( \left( A \cap B \right) \cap C = A \cap \left( B \cap C \right) \)이다. 아래 그림은 벤다이어그램을 통해 결합법칙을 나타낸 그림이다.

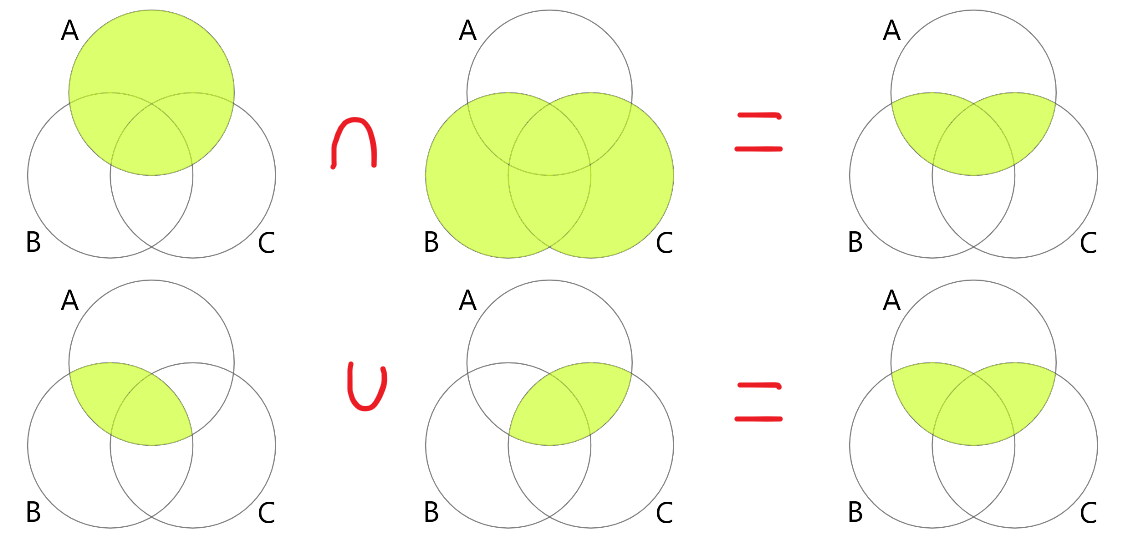
분배법칙
세 집합 \( A \), \( B \), \( C \)에 대하여 \( A \cup \left( B \cap C \right) = \left( A \cup B \right) \cap \left( A \cup C \right) \), \( A \cap \left( B \cup C \right) = \left( A \cap B \right) \cup \left( A \cap C \right) \)이다. 아래 그림은 벤다이어그램을 통해 나타낸 분배법칙이다.

우리는 교집합과 합집합에 대해 성립하는 이 세 가지 연산법칙을 이용해 집합에 대해 다양한 연산을 수행할 수 있다.
그 어떤 것에 대해서라도, 오래간 당연한 것으로 받아들였던 생각들에 가끔씩 물음표를 달아보는 건 바람직한 일이다.
-버트란드 러셀
'수학 > 고등학생을 위한 수학' 카테고리의 다른 글
| 집합과 명제(13) (0) | 2021.05.26 |
|---|---|
| 집합과 명제(12) (0) | 2021.05.25 |
| 대수(7) (0) | 2021.05.23 |
| 대수(6) (0) | 2021.05.22 |
| 집합과 명제(10) (0) | 2021.05.19 |

