※본 글에는 수식이 사용되었습니다. 모바일에서는 수식이 깨져 보이지 않을 수 있는 점 참고 바랍니다. 만일 수식이 깨져 보일 경우 데스크톱 모드를 사용하여 주시길 부탁드립니다.
유리함수

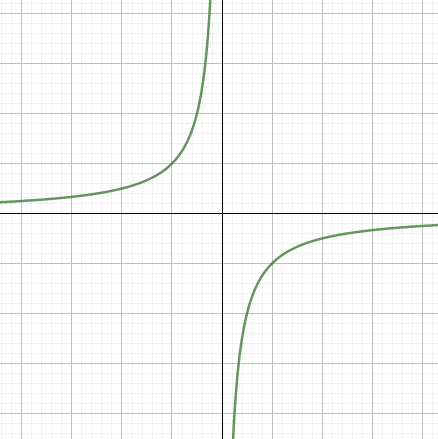
유리함수는 유리식, 즉 분모에 다항식이 있는 함수를 말한다. 그림에 있는 유리함수는 특별히 그 그래프의 계형이 쌍곡선을 나타내는 함수이다. 고등학교 1학년 '수학'에서 이를 배우므로 아마도 고등학생들에게 유리함수가 뭐냐고 물으면 가장 먼저 떠오르는 함수일 것이다. 본문에서도 이 유리함수에 대하여 다룰 것이다.
유리함수의 표현
유리함수는 아래의 식으로 표현할 수 있다.
$$ y-q = \frac{ k }{ x-p } \text{, } y = \frac{cx+d}{ax+b} $$
이러한 유리함수의 그래프는 쌍곡선을 나타내고, 두 직선을 점근선으로 가진다. 특히 \( y=frac{ k }{ x-p }+q \) 꼴의 유리함수의 그래프는 \( x=p \)와 \( y=q \)로 나타나는 두 직선을 점근선으로 가진다. 또한 유리함수의 정의역이 특별히 주어지지 않았을 경우, 유리함수의 분모가 0이 되지 않게 하는 실수 전체를 정의역으로 한다.
\( y = \frac{ k }{x-p}+q \) \( \left( k\ne 0 \right) \)의 성질
유리함수 \( y = \frac{ k }{x-p}+q \) \( \left( k\ne 0 \right) \)는 몇 가지 성질을 지닌다. 이 유리함수는 점 \( \left( p \text{, } q \right) \)에 대하여 함수의 그래프가 대칭이다. 또한 점 \( \left( p \text{, } q \right) \)을 지나고 기울기가 1인 직선과 점 \( \left( p \text{, } q \right) \)을 지나고 기울기가 -1인 직선에 대하여도 함수의 그래프가 대칭을 이룬다.
\( k \)의 부호에 따라서도 그래프의 계형이 달라진다. 점근선을 좌표평면의 두 축처럼 생각할 때, \( k \)가 양수이면 함수의 그래프가 제 1사분면과 제 3사분면에 위치하게 된다. 반대로 \( k \)가 음수이면 함수의 그래프가 제 2사분면과 제 4사분면을 위치하게 된다.
대칭은 인류가 오랜 시간 동안, 그를 통해 질서, 미, 완벽함과 같은 것들을 이해하고 창조하기 위해 노력했던 관념 중의 하나이다.
-헤르만 바일

