반응형
※본 글에는 수식이 사용되었습니다. 모바일에서는 수식이 깨져 보이지 않을 수 있는 점 참고 바랍니다. 만일 수식이 깨져 보일 경우 데스크톱 모드를 사용하여 주시길 부탁드립니다.
이전에 다룬 함수는 대응관계에 따라 구분지어졌다. 그로 인해 이들은 수가 아닌 다른 것을 원소로 가지는 집합들을 가지고도 함수 관계를 만들어 줄 수 있었다. 그러나 본문에서 다룰 함수는 다르다. 본문에서 다룰 함수는 수를 원소로 가지는 집합에서만 정의할 수 있는 함수이다.
우함수
우함수는 함수 \( f \)의 정의역에 속한 모든 \( x \)에 대하여 \( f(x) = f(-x) \)를 만족하는 함수 \( f \)를 말한다. 우함수의 그래프를 좌표평면 상에 아래 그림처럼 나타낼 수 있다.
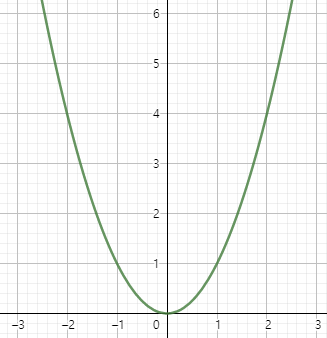

그림에서 볼 수 있듯이 좌표평면 상에서 우함수의 그래프는 x축에 대하여 대칭인 그래프가 된다.
기함수
기함수는 함수 \( f \)의 정의역에 속한 모든 \( x \)에 대하여 \( f(x) = f(-x) \)를 만족하는 함수 \( f \)를 말한다. 기함수의 그래프를 좌표평면 상에 아래 그림처럼 나타낼 수 있다.


그림에서 볼 수 있듯이 좌표평면 상에서 기함수의 그래프는 원점에 대하여 대칭인 그래프가 된다.
그거야 당연히 라마누잔을 발견한 일이지.
-하디
("선생님이 남긴 업적 중에서 가장 대단한 것이 무엇입니까?"에 대한 하디의 답. 라마누잔은 하디의 제자이다.)
반응형


