※본 글에는 수식이 사용되었습니다. 모바일에서는 수식이 깨져 보이지 않을 수 있는 점 참고 바랍니다. 만일 수식이 깨져 보일 경우 데스크톱 모드를 사용하여 주시길 부탁드립니다.
이전에 함수라는 개념을 정의할 때 두 집합의 원소 간 대응 관계를 이용하여 정의했다. 그렇다면 세 집합 \( X \), \( Y \), \( Z \)에 대하여 두 함수 관계 \( X \to Y \), \( Y \to Z \)를 결합하여 \( X \to Y \to Z \)라는 새로운 함수를 만들고 어떻게 표현할 수 있을까? 이를 위해 합성함수라는 새로운 개념을 이용한다.
합성함수
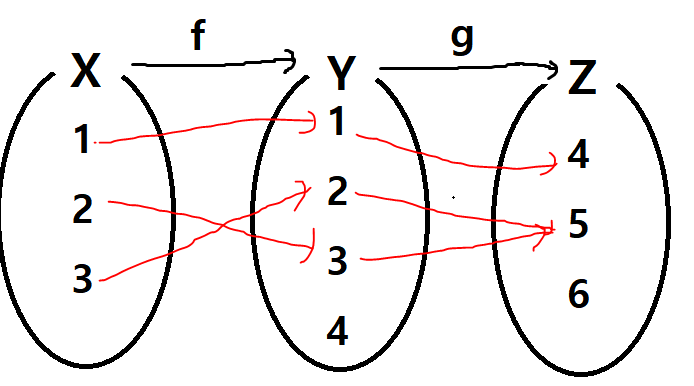
합성함수는 둘 이상의 함수를 합성하여 만든 함수이다. 함수 \( f \): \( X \to Y \)에 대하여 함수 \( f \)의 치역 \( f(X) \)을 새로운 정의역으로 하는 함수 \( g \): \( f(X) \overset{ g }{ \to } Z \)를 정의할 때, 두 함수 \( f \), \( g \)를 이용해 만든 대응 관계 \( h \): \( X \overset{ f }{ \to } f(X) \overset{ g }{ \to } Z \)를 합성함수 \( h = g \circ f \)라고 한다. 여기서 \( \circ \) 기호는 함수를 합성하는 연산자로 쓰이며, 흔히 dot라고 읽는다. 독립변수 \( x \)를 이용하여 나타내면 \( h(x)= \left( g \circ f \right)(x) \)로 나타낼 수 있다.
합성함수의 표현
합성함수 \( h=f \circ g \)는 주로 아래와 같이 표현한다.
\( h = f \circ g \), \( h(x) = \left( f \circ g \right) (x) \), \( h(x) = f \left( g(x) \right) \)
수학은 일정한 규칙에 따라 무의미한 기호를 나열하는 게임이다.
-힐베르트


