※본 글에는 수식이 사용되었습니다. 모바일에서는 수식이 깨져 보이지 않을 수 있는 점 참고 바랍니다. 만일 수식이 깨져 보일 경우 데스크톱 모드를 사용하여 주시길 부탁드립니다.
먼저 함수란 무엇인가 알아보자. 함수란 어떤 집합 내의 각 원소를 다른 집합의 유일한 원소와 대응시키는 관계를 말한다. 즉, 함수 \( f \): \( X \to Y \)는 다음과 같이 정의된다.
| 두 집합 \( X \), \( Y \)와 \( f \in X \times Y \)에 대하여 ① \( \forall x \in X \), \( \exists y \in Y \) \( s.t. \) \( \left( x \text{, } y \right) \in f \) ② \( \left( x \text{, } y_{1} \right) \in f \)이고 \( \left( x \text{, } y_{2} \right) \in f \)이면 \( y_{1} = y_{2} \) 두 조건 ①, ② 모두를 만족하면 \( f \): \( X \to Y \)라고 정의한다. |
조건 ①에서는 함수의 임의성을 말한다. 학생들에게 함수가 무엇이냐 물어보면 'y=f(x) 식으로 표현되는 것', '곡선' 등 다양한 답이 나온다. 조건 ①에서 이러한 질문에 대하여 답을 해준다. 조건 ①에서 '집합 \( X \)의 임의의 원소 \( x \)에 대응되는 집합 \( Y \)의 원소 \( y \)가 존재한다'고 기술된다. 즉, 함수는 어떤 특별한 표현에 의해 기술되거나, 어떤 규칙성을 따르거나, 특별한 형태를 가진 그래프에 의하여 묘사될 필요가 없고, 임의의 대응의 개념으로 정의되어야 한다.
조건 ②에서는 함수의 일가성을 말한다. 함수의 일가성은 함수와 함수가 아닌 것을 구분하는 기준이 되는 것으로 정의역의 각 원소에 대하여 공역의 단 하나의 원소가 대응된다는 말이다.

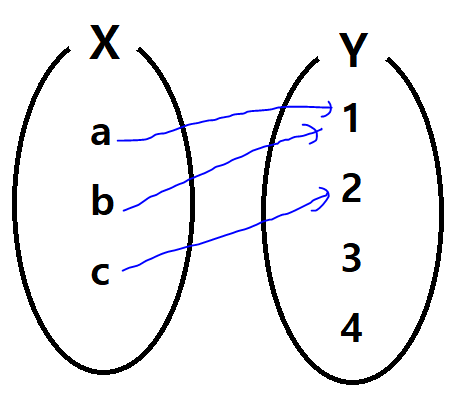
위 그림의 대응 관계는 함수이다. 다만 아래 그림의 대응 관계는 모두 함수가 아니다.

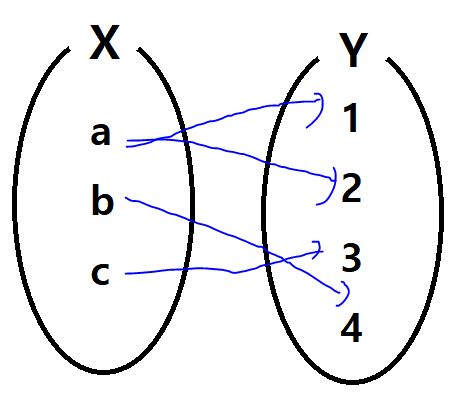
좌측의 그림은 집합 \( X \)의 원소 \( c \)에 대한 대응 관계가 정의되지 않아 조건 ①을 위배하며, 우측의 그림은 집합 \( X \)의 원소 \( a \)에 대응되는 집합 \( Y \)의 원소가 1, 2로 둘이므로 조건 ②를 위배한다. 그러므로 두 그림의 대응 관계는 모두 함수가 아니다.
함수 \( f \): \( X \to Y \)가 정의될 때, 집합 \( X \)를 함수가 정의되는 영역이라 하여 함수 \( f \)의 정의역, 집합 \( Y \)를 함수 \( f \)의 공역이라고 한다. 또한 다음과 같이 정의되는 집합을 함수 \( f \)의 치역이라고 한다.
| \( f(X) = \left\{ f(x)| x \in X \right\} \) |
이 정의에 의하여 치역은 공역의 부분집합이 된다.
이 세상에 배우는 지식 중에서 천국에까지 우리들은 함께 있다고 생각되는 것은 오직 수학뿐이다.
-오스븐

