※본 글에는 수식이 사용되었습니다. 모바일에서는 수식이 깨져 보이지 않을 수 있는 점 참고 바랍니다. 만일 수식이 깨져 보일 경우 데스크톱 모드를 사용하여 주시길 부탁드립니다.
경우의 수를 구하는 문제 유형 중 최단거리의 가짓수를 구하는 유형이 있다. 이 유형을 푸는 방법은 크게 두 가지로 나뉜다. 하나는 같은 것이 있는 순열을 이용하는 것이고, 또 다른 하나는 노가다이다. 필자는 이 두 방법 중 노가다를 더 선호한다. 아래 그림처럼 길을 따라갈 때, 지점 A에서 지점 B까지 최단거리로 가는 경우의 수를 구해보자.

같은 것이 있는 순열
먼저 주어진 조건에 맞추어 갈 수 있는 길의 방향과 그의 개수를 확인한다. 여기서는 위로 가는 방향(↑) 12개와 우측으로 가는 방향(→) 17개만을 사용해서 가야만 A에서 B까지 최단거리로 갈 수 있다. 그러므로 길을 가는 방향의 순서를 결정하는 방법을 정해주는 개수가 곧 A에서 B까지 최단거리로 가는 가짓수가 된다. 길을 가는 방향의 순서의 가짓수는 총 29개의 방향으로 만드는 순열, 즉 같은 것이 있는 순열의 수와 동일하므로 구하는 경우의 수는 아래와 같다.
$$ \frac{ 29! }{ 12! \times 17! } $$
장애물이 있거나 길이 나타난 판이 직사각형이 아닌 경우에도 case를 나누어 각각 경우의 수를 구해준 후, 각 경우의 수를 더하거나 빼거나 곱하여 원하는 결괏값을 도출해내면 된다.
노가다
노가다를 통해 경우의 수를 구하는 방법은 매우 간단하다. 또한 정확도가 매우 높다. 같은 것이 있는 순열을 이용하여 경우의 수를 구하면 case를 나누어 구해주어야 하는 경우가 매우 많기에 잘못된 값을 도출해내는 경우를 많이 봤다. 물론 실수로 인한 결과이다. 그러나 이 방법은 단순 덧셈과 곱셈만을 이용해 하나하나의 경우를 일일이, 그리고 한 번에 구해내기에 실수할 가능성이 줄어든다. 물론 그래도 실수할 사람은 실수한다. 위 그림의 일부분만을 사용하여 그 부분까지만 이 방법을 통하여 경우의 수를 구해보겠다.

먼저 A에서 바로 오른쪽 또는 위로 최단거리로 가는 경우의 수는 1가지뿐이다. 그러므로 이처럼 최단거리로 가는 경우의 수가 1가지인 갈림길에 모두 1을 표기한다.

자 이제 최단거리로 가는 길의 수가 오직 한 가지가 아닌 갈림길만이 남았다. 이 길들은 모두 다른 길로부터 이어져 있으며, 임의의 갈림길에 대하여 우측이나 위쪽으로 오는 길로 이어지는 부분, 그 두 부분으로 가는 시작점이 되는 갈림길까지 가는 경우의 수의 합이 그 임의의 갈림길까지 가는 경우의 수가 된다. 글로는 이해하기 힘드니 아래 표의 그림을 보며 이해하기 바란다.
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
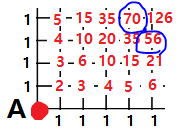 |
도착하기 원하는 지점까지 이 과정을 반복하면 원하는 경우의 수를 구할 수 있다. 흔히 문제로 나오는 유형은 구하는 경우의 수가 그리 크지 않기 때문에 대부분은 이 방법으로 쉽게 해결할 수 있다. 또한 경우의 수가 많아도 이 방법이 먹히지 않는 것은 아니다. 오히려 그럴 경우엔 이 방법이 정확한 값을 도출해낼 확률이 더 높을 수 있다.
인간의 지식은 모두 직관으로부터 시작하여 개념으로 나아가서 아이디어로 끝난다.
-칸트



