※본 글에는 수식이 사용되었습니다. 모바일에서는 수식이 깨져 보이지 않을 수 있는 점 참고 바랍니다. 만일 수식이 깨져 보일 경우 데스크톱 모드를 사용하여 주시길 부탁드립니다.
중학교에서 삼각형의 넓이를 구하는 공식에 대해 배워 본 경험이 있을 것이다. 그 공식을 응용하여 삼각형의 한 변의 길이나 높이 등을 구하라는 문제가 많았다. 중학교 교과과정에서 배우는 것만을 사용하여 문제를 풀면 식이 상당히 복잡하고 계산 과정이 매우 귀찮다. 그래서 필자는 중학생 때 헤론의 공식을 자주 사용했으나, 이에 대한 증명을 알지는 못하였다. 본문에서는 헤론의 공식에 대하여 알아볼 것이다.
헤론의 공식
우리가 삼각형의 넓이를 구하기 위해서는 본래 삼각형의 한 변의 길이와 그 변에 대한 삼각형의 높이를 알아야 한다. 그러나 앞서 우리는 삼각형의 높이를 알지 못하여도 삼각형의 다른 성분으로부터 삼각형의 넓이를 유도해낼 수 있는 여러 공식들을 배워왔다. 특히 삼각형의 두 변의 길이와 그 사이에 끼인 각을 알때 사용하는 공식1은 SAS 합동으로 나오는 경우, 삼각형의 넓이를 더 이상의 다른 정보 없이 구할 수 있게 해준다. 헤론의 공식은 SSS 합동인 경우, 삼각형의 넓이를 구할 수 있게 해준다. 즉, 세 변의 길이만으로 삼각형의 넓이를 표현할 수 있다. 삼각형 ABC의 넓이를 S라고 할 때, 헤론의 공식은 다음과 같이 서술된다.
$$ S = \sqrt{ s \left( s-a \right) \left( s-b \right) \left( s-c \right) } \text{ } \left( s = \frac{a+b+c}{2} \right) $$
헤론의 공식은 그 역사가 아주 오래인 만큼 다양한 증명이 있다. 본문에서는 그 중 두 가지 증명법에 대해 다루고자 한다.
코사인 법칙을 이용한 증명
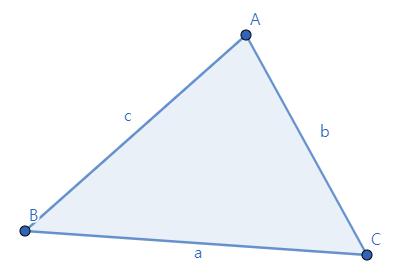
삼각형 ABC에 대하여 각 A를 θ라고 하면, 코사인 법칙에 의하여 다음 등식이 성립한다.
$$ \cos{\theta} = \frac{ b^{2} +c^{2} -a^{2} }{ 2bc } $$
0<θ<π이므로
$$ \begin{matrix} \sin{\theta} &=& \sqrt{ 1-\cos^{2}{\theta} } \\ &=& \sqrt{ 1-\left( \frac{ b^{2} +c^{2} -a^{2} }{ 2bc } \right)^{2} } \\ &=& \sqrt{ \frac{ 4b^{2}c^{2} -\left( b^{2} +c^{2} -a^{2} \right) }{ 4b^{2}c^{2} } } \\ &=& \sqrt{ \frac{ \left( 2bc +b^{2} +c^{2} -a^{2} \right) \left( 2bc -b^{2} -c^{2} +a^{2} \right) }{ 4b^{2}c^{2} } } \\ &=& \sqrt{ \frac{ \left\{ \left( b+c \right)^{2} -a^{2} \right\} \left\{ a^{2} -\left( b-c \right) \right\} }{ 4b^{2}c^{2} } } \\ &=& \sqrt{ \frac{ \left( a+b+c \right) \left( b+c-a \right) \left( a+b-c \right) \left( a-b+c \right) }{ 4b^{2}c^{2} } } \\ &=& \sqrt{ \frac{ \left( a+b+c \right) \left( a+b+c-2a \right) \left( a+b+c-2c \right) \left( a+b+c-2b \right) }{ 4b^{2}c^{2} } } \end{matrix} $$
$$ \text{이때 } S = \frac{1}{2} bc \sin{\theta} \text{이므로} $$
$$ \begin{matrix} S &=& \frac{1}{2} bc \sqrt{ \frac{ \left( a+b+c \right) \left( a+b+c-2a \right) \left( a+b+c-2c \right) \left( a+b+c-2b \right) }{ 4b^{2}c^{2} } } \\ &=& \sqrt{ \frac{ \left( a+b+c \right) \left( a+b+c-2a \right) \left( a+b+c-2c \right) \left( a+b+c-2b \right) }{ 16 } } \\ &=& \sqrt{ \frac{ a+b+c }{ 2 } \left( \frac{ a+b+c -2a }{ 2 } \right) \left( \frac{ a+b+c -2b }{ 2 } \right) \left( \frac{ a+b+c -2c }{ 2 } \right) } \end{matrix} $$
$$ \frac{a+b+c}{2} = s \text{라고 두면} $$
$$ S = \sqrt{ s \left( s-a \right) \left( s-b \right) \left( s-c \right) } $$
피타고라스의 정리를 이용한 증명

삼각형 ABC에 대하여 꼭짓점 A에서 섭분 BC에 내린 수선의 발을 H라고 하고, 선분 AH의 길이를 h, 선분 BH의 길이를 p라고 하면 선분 CH의 길이는 (a-p)가 된다. 피타고라스의 정리에 의하여
$$ \overline{AB}^{2} = \overline{BH}^{2} +\overline{AH}^{2} \text{, } \overline{AC}^{2} = \overline{AH}^{2} +\overline{HC}^{2} \text{이므로} $$
$$ c^{2} = p^{2}+h^{2} \text{, } b^{2} = h^{2} +\left( a-p \right)^{2} $$
$$ b^{2} = h^{2} +a^{2}-2ap+p^{2} $$
( b^{2}=h^{2}+a^{2}-2ap+p^{2} )에서 ( c^{2}=p^{2}+h^{2} )을 빼주면
$$ b^{2}-c^{2} = a^{2} -2ap $$
$$ p = \frac{ a^{2} -b^{2} +c^{2} }{ 2a } $$
위 식을 c^{2} = p^{2}+h^{2}에 대입하면
$$ c^{2} = \left( \frac{ a^{2} -b^{2} +c^{2} }{ 2a } \right)^{2} +h^{2} $$
$$ h^{2} = c^{2} -\left( \frac{ a^{2} -b^{2} +c^{2} }{ 2a } \right)^{2} $$
$$ h^{2} = \left( c +\frac{ a^{2} -b^{2} +c^{2} }{ 2a } \right) \left( c -\frac{ a^{2} -b^{2} +c^{2} }{ 2a } \right) $$
$$ h = \sqrt{ \left( c +\frac{ a^{2} -b^{2} +c^{2} }{ 2a } \right) \left( c -\frac{ a^{2} -b^{2} +c^{2} }{ 2a } \right) } $$
삼각형 ABC의 넓이를 S라고 하면
$$ S = \frac{1}{2}ah \text{이므로} $$
$$ \begin{matrix} S &=& \frac{1}{2} a \sqrt{ \left( c +\frac{ a^{2} -b^{2} +c^{2} }{ 2a } \right) \left( c -\frac{ a^{2} -b^{2} +c^{2} }{ 2a } \right) } \\ &=& \sqrt{ \frac{a^{2}}{4} \left( c +\frac{ a^{2} -b^{2} +c^{2} }{ 2a } \right) \left( c -\frac{ a^{2} -b^{2} +c^{2} }{ 2a } \right) } \\ &=& \sqrt{ \frac{ \left( 2ac+a^{2}-b^{2}+c^{2} \right) \left( 2ac -a^{2}+b^{2}-c^{2} \right) }{ 16 } } \\ &=& \sqrt{ \frac{ \left\{ \left( a+c \right)^{2} -b^{2} \right\} \left\{ b^{2} -\left( a-c \right)^{2} \right\} }{ 16 } } \\ &=& \sqrt{ \frac{ \left( a+b+c \right) \left( a+c-b \right) \left( a+b-c \right) \left( b+c-a \right) }{ 16 } } \\ &=& \sqrt{ \frac{ \left( a+b+c \right) \left( a+b+c-2a \right) \left( a+b+c-2c \right) \left( a+b+c-2b \right) }{ 4b^{2}c^{2} } } \\ &=& \sqrt{ \frac{ \left( a+b+c \right) \left( a+b+c-2a \right) \left( a+b+c-2c \right) \left( a+b+c-2b \right) }{ 16 } } \\ &=& \sqrt{ \frac{ a+b+c }{ 2 } \left( \frac{ a+b+c -2a }{ 2 } \right) \left( \frac{ a+b+c -2b }{ 2 } \right) \left( \frac{ a+b+c -2c }{ 2 } \right) } \end{matrix} $$
$$ \frac{a+b+c}{2} = s \text{라고 두면} $$
$$ S = \sqrt{ s \left( s-a \right) \left( s-b \right) \left( s-c \right) } $$
이외에도 좌표평면을 이용하는 등 다양한 방법으로 헤론의 공식을 증명할 수 있다.
문외한들의 비이성적인 생각과 달리 계산 체계의 선택은 단순히 관례의 문제이다.
-파스칼
- S=1/2 ab sin θ [본문으로]
'수학 > 고등학생을 위한 수학' 카테고리의 다른 글
| 삼각함수(11) (0) | 2021.03.19 |
|---|---|
| 확률과 통계(13) (0) | 2021.03.18 |
| 삼각함수(9) (0) | 2021.03.16 |
| 확률과 통계(12) (0) | 2021.03.15 |
| 삼각함수(8) (0) | 2021.03.14 |



