※본 글에는 수식이 사용되었습니다. 모바일에서는 수식이 깨져 보이지 않을 수 있는 점 참고 바랍니다. 만일 수식이 깨져 보일 경우 데스크톱 모드를 사용하여 주시길 부탁드립니다.
<고등학생을 위한 수학 - 삼각함수(5)>에서 삼각함수의 성질 중 임의의 각에 대하여 직각의 정수배를 더해주었을 때 삼각함수의 값이 어떻게 변화하는지 알아보았다. 본문에서는 이를 일반화한 정리인 삼각함수의 덧셉정리에 대하여 알아볼 것이다.
삼각함수의 덧셈정리
$$ \cos{ \left( \alpha +\beta \right) } = \cos{ \alpha } \cos{ \beta } -\sin{ \alpha } \sin{ \beta } $$
$$ \cos{ \left( \alpha -\beta \right) } = \cos{ \alpha } \cos{ \beta } +\sin{ \alpha } \sin{ \beta } $$
$$ \sin{ \left( \alpha +\beta \right) } = \sin{ \alpha } \cos{ \beta } +\cos{ \alpha } \sin{ \beta } $$
$$ \sin{ \left( \alpha -\beta \right) } = \sin{ \alpha } \cos{ \beta } -\cos{ \alpha } \sin{ \beta } $$
$$ \tan{ \left( \alpha +\beta \right) } = \frac{ \tan{ \alpha } +\tan{ \beta } }{ 1-\tan{ \alpha } \tan{ \beta } } $$
$$ \tan{ \left( \alpha -\beta \right) } = \frac{ \tan{ \alpha } -\tan{ \beta } }{ 1+\tan{ \alpha } \tan{ \beta } } $$
삼각함수의 덧셈정리는 임의의 한 각을 더해주었을 때, 삼각함수의 값의 변화를 임의의 두 각의 합과 차로 일반화한 정리이다. 즉, 이 정리를 이용하면 우리가 알고 있는 특수각을 적당히 이용하여 여러 크기의 각의 삼각비 값을 알아낼 수 있게 된다. 아래는 sin, cos, tan 함수의 덧셈정리를 증명하는 과정이다.
cos의 경우
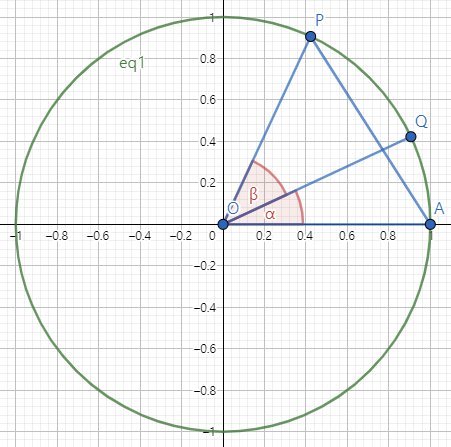

먼저 위 그림과 같이 단위원에 두 각 α와 β를 그리자. 선분 AP의 길이는 선분 QR의 길이와 같고,
$$ \overline{AP} = \sqrt{ \left\{ \cos{ \left( \alpha +\beta \right) }-1 \right\}^{2} +\sin^{2}{ \left( \alpha +\beta \right) } } \text{, } $$
$$ \overline{QR} = \sqrt{ \left( \cos{\alpha} -\cos{\beta} \right)^{2} +\left( \sin{\alpha} +\sin{\beta} \right)^{2} } \text{이므로} $$
$$ \left\{ \cos{ \left( \alpha +\beta \right) }-1 \right\}^{2} +\sin^{2}{ \left( \alpha +\beta \right) } = \left( \cos{\alpha} -\cos{\beta} \right)^{2} +\left( \sin{\alpha} +\sin{\beta} \right)^{2} $$
$$ \begin{matrix} \cos^{2}{ \left( \alpha +\beta \right) } -2 \cos{ \left( \alpha +\beta \right) } +1 +\sin^{2}{ \left( \alpha +\beta \right) } &=& \cos^{2}{ \alpha } -2 \cos{ \alpha } \cos{ \beta } +\cos^{2}{ \beta } \\ & & +\sin^{2}{ \alpha } +2 \sin{ \alpha } \sin{ \beta } +\sin^{2}{ \beta } \end{matrix} $$
$$ \text{이때 } \sin^{2}{ \theta } +\cos^{2}{ \theta } = 1 \text{이므로} $$
$$ 2 -2 \cos{ \left( \alpha +\beta \right) } = 2 -2 \cos{ \alpha } \cos{ \beta } +2 \sin{ \alpha } \sin{ \beta } $$
$$ \therefore \cos{ \left( \alpha +\beta \right) } = \cos{ \alpha } \cos{ \beta } -\sin{ \alpha } \sin{ \beta } $$
이 식의 β 자리에 -β를 대입하면 다음 등식이 성립한다.
$$ \cos{ \left( \alpha -\beta \right) } = \cos{ \alpha } \cos{ \beta } +\sin{ \alpha } \sin{ \beta } $$
필자는 이 cos 함수의 덧셈정리를 '코코 싸싸'로 외웠다.
sin의 경우
sin 함수의 덧셈정리는 cos 함수의 덧셈정리로부터 유도할 수 있다.
$$ \cos{ \left( \frac{\pi}{2} -\theta \right) } = \sin{\theta} \text{이므로} $$
$$ \cos{ \left( \frac{\pi}{2} -\alpha -\beta \right) } = \cos{ \left\{ \frac{\pi}{2} -\left( \alpha +\beta \right) \right\} } = \sin{ \left( \alpha +\beta \right) } $$
$$ \begin{matrix} \sin{ \left( \alpha +\beta \right) } &=& \cos{ \left\{ \frac{\pi}{2} -\left( \alpha +\beta \right) \right\} } \\ &=& \cos{ \left\{ \left( \frac{\pi}{2} -\alpha \right) -\beta \right\} } \\ &=& \cos{ \left( \frac{ \pi }{ 2 } +\alpha \right) } \cos{ \beta } -\sin{ \left( \frac{ \pi }{ 2 } -\alpha \right) } \sin{\beta} \\ &=& \sin{ \alpha } \cos{ \beta } +\cos{ \alpha } \sin{ \beta } \end{matrix} $$
$$ \therefore \sin{ \left( \alpha +\beta \right) } = \sin{ \alpha } \cos{ \beta } +\cos{ \alpha } \sin{ \beta } $$
이 식의 β 자리에 -β를 대입하면 다음 등식이 성립한다.
$$ \sin{ \left( \alpha -\beta \right) } = \sin{ \alpha } \cos{ \beta } -\cos{ \alpha } \sin{ \beta } $$
필자는 이 sin 함수의 덧셈정리를 '싸코 코싸'로 외웠다.
tan의 경우
$$ \begin{matrix} \tan{ \left( \alpha +\beta \right) } &=& \frac{ \sin{ \left( \alpha +\beta \right) } }{ \cos{ \left( \alpha +\beta \right) } } \\ &=& \frac{ \sin{ \alpha } \cos{ \beta } +\cos{ \alpha } \sin{ \beta } }{ \cos{ \alpha } \cos{ \beta } -\sin{ \alpha } \sin{ \beta } } \\ &=& \frac{ \frac{ \sin{ \alpha } \cos{ \beta } +\cos{ \alpha } \sin{ \beta } }{ \cos{ \alpha } \cos{ \beta } } }{ \frac{ \cos{ \alpha } \cos{ \beta } -\sin{ \alpha } \sin{ \beta } }{ \cos{ \alpha } \cos{ \beta } } } \\ &=& \frac{ \frac{ \sin{ \alpha } }{ \cos{ \alpha } } +\frac{ \sin{ \beta } }{ \cos{ \beta } } }{ 1 -\frac{ \sin{ \alpha } }{ \cos{ \alpha } } \frac{ \sin{ \beta } }{ \cos{ \beta } } } \\ &=& \frac{ \tan{ \alpha } +\tan{ \beta } }{ 1-\tan{ \alpha } \tan{ \beta } } \end{matrix} $$
$$ \therefore \tan{ \left( \alpha +\beta \right) } = \frac{ \tan{ \alpha } +\tan{ \beta } }{ 1-\tan{ \alpha } \tan{ \beta } } $$
이 식의 β 자리에 -β를 대입하면 다음 등식이 성립한다.
$$ \tan{ \left( \alpha -\beta \right) } = \frac{ \tan{ \alpha } -\tan{ \beta } }{ 1+\tan{ \alpha } \tan{ \beta } } $$
필자는 이 tan 함수의 덧셈정리를 '일탄탄 탄플탄', '일탄탄 탄마탄'으로 외웠다.
수학적 논증을 허용하지 않는 한, 어떤 조사도 엄밀하게 과학적이라고 말할 수 없다.
-레오나르도 다 빈치
'수학 > 고등학생을 위한 수학' 카테고리의 다른 글
| 함수(1) (0) | 2021.03.23 |
|---|---|
| 삼각함수(12) (0) | 2021.03.20 |
| 확률과 통계(13) (0) | 2021.03.18 |
| 삼각함수(10) (0) | 2021.03.17 |
| 삼각함수(9) (0) | 2021.03.16 |

