※본 글에는 수식이 사용되었습니다. 모바일에서는 수식이 깨져 보이지 않을 수 있는 점 참고 바랍니다. 만일 수식이 깨져 보일 경우 데스크톱 모드를 사용하여 주시길 부탁드립니다.
본문과 다음 글에서 삼각함수의 두 가지 법칙에 대하여 알아볼 것이다. 먼저 사인 법칙에 대하여 알아보자.
사인 법칙
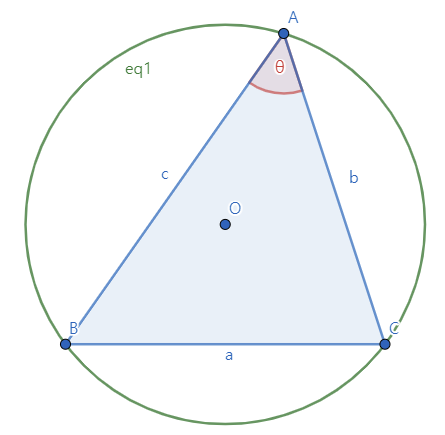
사인 법칙은 삼각형의 변과 그 대각의 sin 값이 이루는 관계를 설명한다. 삼각형 ABC에 대하여 삼각형 ABC의 외접원의 반지름을 R이라고 하면 다음이 성립한다.
$$ \frac{ a }{ \sin{A} } = \frac{ b }{ \sin{B} } = \frac{ c }{ \sin{C} } = 2R $$
위 등식을 사인 법칙이라고 한다. 위의 식을 보면 알 수 있듯이 사인 법칙은 삼각형의 변의 길이와 그 대각의 사인값과 외접원의 반지름의 길이 간의 관계를 나타낸다. 그러므로 사인 법칙을 이용하면 삼각형의 한 변의 길이와 두 각의 크기를 알면 나머지 두 변의 길이를 구할 수 있다. 사인 법칙은 아래 과정을 통해 증명할 수 있다.
증명
사인 법칙을 증명하기에 앞서 각의 크기에 따라 경우를 나눠보자. 삼각형의 세 내각의 크기의 합은 π이므로 직각, 예각, 둔각 세 가지 경우에 대하여 증명하면 모든 삼각형에 대하여 사인 법칙을 적용할 수 있다.


직각인 경우
반지름이 R인 원에 내접하면서 각 A를 직각으로 하는 직각삼각형 ABC를 생각해보자. 빗변 a는 외접원의 지름이 되므로 a=2R이고, sin (π/2)=1이므로
(a)/(sin A)=2R이 성립한다.
예각인 경우
반지름이 R인 원에 내접하는 예각삼각형 ABC를 생각해보자. 동일한 원호에 대한 임의의 원주각의 크기는 항상 같다. 그러므로 원주각의 성질에 의하여 동일한 호 BC에 대한 원주각 A의 크기는 점 A를 이옫시켜도 변하지 않는다. 그러므로 편의를 위해 각 B가 직각이 되도록 점 A만을 원호를 따라 움직여주면 아래의 그림과 같은 직각삼각형을 만들 수 있다.

각 B가 직각이므로 b=2R이 된다. sin의 정의에 의하여
$$ \sin{A} = \frac{ a }{ 2R } $$
$$ \therefore 2R = \frac{ a }{ \sin{A} } $$
둔각인 경우

위 그림과 같이 반지름이 R인 원에 내접하면서 각 A를 둔각으로 하는 둔각삼각형 ABC를 생각해보자. 점 BC에 의하여 원주는 두개의 호로 나뉜다. 이 중 점 A가 위치하지 않은 호 위에 점 A'을 잡아주면 삼각형 A'BC는 예각삼각형이 된다. 그러므로 각 A'에 대하여 사인법칙이 성립한다.
$$ \sin{A^{\prime}} = \frac{ a }{ 2R } $$
이때, A'=π-A이므로
$$ \sin{\left( \pi -A \right)} = \sin{A} $$
$$ \therefore \sin{A} = \frac{ a }{ 2R } $$
각 B, C가 직각, 예각, 둔각인 경우 또한 각 A와 동일한 과정을 통해 증명이 가능하다. 직각, 예각, 둔각인 경우에 대하여 모두 성립하므로 삼각형 ABC에 대하여
$$ \frac{ a }{ \sin{A} } = \frac{ b }{ \sin{B} } = \frac{ c }{ \sin{C} } = 2R \text{은 항상 성립한다.} $$
수학의 매력은 결과가 절대적으로 확실하다는 데 있다.
-루이스 캐럴
'수학 > 고등학생을 위한 수학' 카테고리의 다른 글
| 확률과 통계(12) (0) | 2021.03.15 |
|---|---|
| 삼각함수(8) (0) | 2021.03.14 |
| 삼각함수(6) (0) | 2021.03.12 |
| 확률과 통계(11) (0) | 2021.03.11 |
| 확률과 통계(10) (0) | 2021.03.10 |



