※본 글에는 수식이 사용되었습니다. 모바일에서는 수식이 깨져 보이지 않을 수 있는 점 참고 바랍니다. 만일 수식이 깨져 보일 경우 데스크톱 모드를 사용하여 주시길 부탁드립니다.
벡터를 이용하면 다양한 관계식을 간단히 표현할 수 있다. 본문에서는 직선의 방정식을 벡터를 이용하여 표현하는 법에 대하여 다룰 것이다. 아마 이 글을 독자들에게는 xy 좌표평면에서 표현된 직선의 방정식은 아래의 꼴이 익숙할 것이다.
$$ ax+by+c = 0 $$
자, 지금부터 두 점 A(a_{1}, a_{2}), B(b_{1}, b_{2})를 지나는 직선의 방정식을 벡터를 이용하여 표현해 보자. 먼저 두 점 A, B를 각각 종점으로 하는 위치벡터 a, b를 정의하자.

직선 AB와 기울기가 같은 벡터를 만들어주기 위해 다음의 연산을 수행하자.
$$ \vec{b}-\vec{a} = \left( b_{1}-a_{1} \text{, } b_{2}-a_{2} \right) $$

이 위치벡터의 종점은 단 하나의 점으로 특정이 되므로 적당한 처리를 해주어 직선을 표현하도록 만들어 주자. 위의 식과 같이 표현된 벡터에 스칼라 t를 곱해주면
$$ t \left( \vec{b}-\vec{a} \right) = t \left( b_{1}-a_{1} \text{, } b_{2}-a_{2} \right) $$
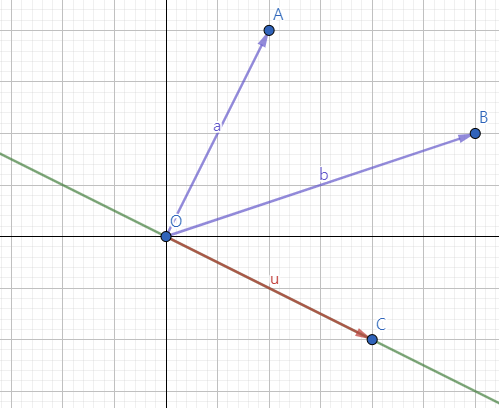
위에서 한 처리, 즉 스칼라 t를 곱해줌으로 인해 이 위치벡터의 종점은 스칼라 t의 값에 의하여 정의되는 직선 AB와 기울기가 같고 원점을 지나는 직선 위의 점 중 하나가 된다. 우리가 구하려는 바는 직선 AB의 방정식이므로 위 관계식에 적당한 처리를 해주어야 한다. 위의 관계식으로 나타나는 직선을 평행이동 시켜주자.
$$ \left( a_{1} \text{, } a_{2} \right) +t \left( \vec{b}-\vec{a} \right) = \left( a_{1} \text{, } a_{2} \right) +t \left( b_{1}-a_{1} \text{, } b_{2}-a_{2} \right) $$

여기서 평행이동을 위해 더해준 점 A의 좌표는 점 B의 좌표로 대체해도 상관없다. 여기서 위치벡터 b-a=u라고 하면 구하는 직선의 방정식은
$$ \left(x \text{, } y \right) = A +t \vec{u} $$
위치벡터 u의 x성분과 y성분을 각각 u_{1}, u_{2}라고 하면 위 직선의 방정식을 다음과 같이 바꿔 쓸 수 있다.
$$ x = a_{1} +t u_{1} \text{, } y = a_{2} + t u_{2} $$
$$ t = \frac{x -a_{1}}{u_{1}} = \frac{y -a_{2}}{u_{2}} $$
직선의 방정식을 사용해야할 상황이 올 경우 y=mx+n 꼴을 포함하여 5가지 형태의 방정식 중 상황에 따라 편한 것을 사용하면 된다.
근본적인 발전은 기초적인 사상을 새롭게 해석할 때에 이루어진다.
-화이트헤드
'수학 > 고등학생을 위한 수학' 카테고리의 다른 글
| 기하와 벡터(26) (0) | 2021.03.02 |
|---|---|
| 기하와 벡터(25) (0) | 2021.03.01 |
| 기하와 벡터(23) (0) | 2021.02.26 |
| 기하와 벡터(22) (0) | 2021.02.26 |
| 확률과 통계(3) (0) | 2021.02.24 |



