※본 글에는 수식이 사용되었습니다. 모바일에서는 수식이 깨져 보이지 않을 수 있는 점 참고 바랍니다. 만일 수식이 깨져 보일 경우 데스크톱 모드를 사용하여 주시길 부탁드립니다.
삼각치환법
삼각치환법은 적분하기 어려운 함수를 삼각함수의 성질1을 이용하여 비교적 간단하게 적분할 수 있도록 해주는 적분법이다. 고등학교에서 삼각치환법은 주로 정적분을 계산하기 위해 사용되는데, 이는 고등학교에서는 arcsin 등의 삼각함수를 배우지 않기 때문이다. 삼각치환법의 종류는 크게 3가지가 있다. 여기서는 이를 세분화하여 6가지로 서술할 것이다.
sin, cos 치환
$$ a>0 \text{에 대하여 } x>a \text{, } x=a\sin{ \theta } \left( -{ {\pi} \over {2} } \le \theta \le { {\pi} \over {2} } \right) \text{라고 하면} $$
$$ \sqrt{ a^{2}-x^{2} } = a\cos{ \theta } \text{, } { {\operatorname{d}\!x} \over {\operatorname{d}\!\theta} } = a\cos{\theta} \text{이므로} $$
$$ \int { { {1} \over { \sqrt{ a^{2}-x^{2} } } } }\, \operatorname{d}\!x = \int { 1 }\, \operatorname{d}\!\theta $$
$$ a>0 \text{에 대하여 } x>a \text{, } x=a\cos{ \theta } \left( 0 \le \theta \le \pi \right) \text{라고 하면} $$
$$ \sqrt{ a^{2}-x^{2} } = a\sin{ \theta } \text{, } { {\operatorname{d}\!x} \over {\operatorname{d}\!\theta} } = -a\sin{\theta} \text{이므로} $$
$$ \int { { {1} \over { \sqrt{ a^{2}-x^{2} } } } }\, \operatorname{d}\!x = \int { \left( -1 \right) }\, \operatorname{d}\!\theta $$
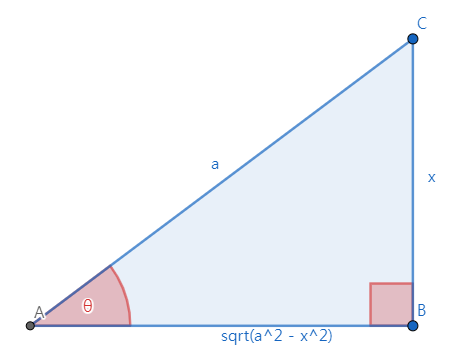
sin 치환
삼각치환법을 알아보기 위해 예를 들어보자.2 다음과 같은 형식의 적분을 생각해보자.
$$ \int { { {1} \over {\sqrt{ a^{2}-x^{2} }} } }\, \operatorname{d}\!x $$
$$ x = a \sin{\theta} \left( -{ {\pi} \over {2} } \le \theta \le { {\pi} \over {2} } \right) \text{라고 두면} $$
이와 같이 치환을 하고 theta의 범위를 잡아주는 이유는
1. sin^{2} θ+cos^{2} θ=1이라는 삼각항등식을 이용하기 위해서이다. 이 삼각항등식을 정리하면 1-sin^{2} θ=cos^{2} θ가 되므로 sqrt{ 1-sin^{2} θ }=cos θ가 된다.
2. sin 함수는 주기함수이며, 일대일함수가 아니므로 치역 내의 어떤 함숫값에 대응하는 정의역 내 원소는 일반적으로 무수히 많다. 그러므로 이와 같이 θ의 범위를 잡아주는 것은 sin 함수를 일대일함수으로 만들어주는 효과를 준다.
이다.
$$ \sqrt{ a^{2}-x^{2} } = \sqrt{ a^{2} \left( 1-\sin^{2}{\theta} \right) } = a \cos{\theta} \text{, } { {\operatorname{d}\!x} \over {\operatorname{d}\!\theta} } = a \cos{\theta} \text{이므로} $$
위에서 설명했듯이 sin^{2} θ+cos^{2} θ=1이므로 sqrt{ 1-sin^{2} θ }=cos θ이다.
$$ \int { { {1} \over {\sqrt{ a^{2}-x^{2} }} } }\, \operatorname{d}\!x = \int { { {1} \over {a \cos{\theta}} } }\, \operatorname{d}\!x = \int { { {1} \over {a \cos{\theta}} } \cdot { {\operatorname{d}\!x} \over {\operatorname{d}\!\theta} } }\, \operatorname{d}\!\theta $$
앞서 나온 식들을 적분에 대입하여 정리한 식이다. 이때, 피적분식3을 θ로 정리하였으니 적분변수 또한 θ로 정리해주어야 한다. 여기서 dx/dθ는 적분변수를 θ로 바꾸어주기 위해 사용한 것이다. 여기서 특이한 점이 있다. 일반적으로 치환적분법을 사용할 때에는 피적분식에서 속미분 식을 없애줌과 달리 삼각치환법에서는 피적분식에 속미분식을 집어넣어준다. 즉, 일반적인 치환적분법과 달리 삼각치환법에서는 치환적분법을 역으로 이용한 것이다. 물론 치환적분법을 이용해 유도하는 것도 가능하나, 본래는 역삼각함수를 배워야 가능한 방법이다.
$$ \int { { {1} \over {a \cos{\theta}} } \cdot { {\operatorname{d}\!x} \over {\operatorname{d}\!\theta} } }\, \operatorname{d}\!\theta = \int { { {1} \over {a \cos{\theta}} } \cdot a \cos{\theta} }\, \operatorname{d}\!\theta = \int { 1 }\, \operatorname{d}\!\theta $$
앞서 정리한 식에서 dx/dθ에 a cos θ를 대입하고 정리하면 약분되어 피적분식이 1이 된다. 즉, 이 부분은 대입하고 식을 정리해주는 과정이다.
$$ \int {1}\, \operatorname{d}\!\theta = \theta+C \left( C \text{는 적분상수} \right) $$
최종적으로 θ에 관한 부정적분 식이 나오게 된다. 이를 다시 x에 관한 식으로 정리하기 위해서는 역삼각함수에 대해 알고 있어야 한다. 역삼각함수에 대해서 고등학교에서는 다루지 않으므로 이후 기회가 되다면 다루도록 하겠다.
cos 치환
위에서 밝혔듯이 cos 치환도 예를 통해 알아볼 것이다.
$$ \int { { {1} \over {\sqrt{ a^{2}-x^{2} }} } }\, \operatorname{d}\!x $$
$$ x = a \cos{\theta} \left( 0 \le \theta \le \pi \right) \text{라고 두면} $$
이와 같이 치환을 하고 θ의 범위를 잡아주는 이유는
1. sin^{2} θ+cos^{2} θ=1이라는 삼각항등식을 이용하기 위해서이다. 이 삼각항등식을 정리하면 1-cos^{2} θ=sin^{2} θ가 되므로 sqrt{ 1-cos^{2} θ }=sin θ가 된다.
2. cos 함수는 주기함수이며, 일대일함수가 아니므로 치역 내의 어떤 함숫값에 대응하는 정의역 내 원소는 일반적으로 무수히 많다. 그러므로 이와 같이 θ의 범위를 잡아주는 것은 cos 함수를 일대일함수로 만들어주는 효과를 준다.
이다.
$$ \sqrt{ a^{2}-x^{2} } = \sqrt{ a^{2} \left( 1-\cos^{2}{\theta} \right) } = a \sin{\theta} \text{, } { {\operatorname{d}\!x} \over {\operatorname{d}\!\theta} } = -a \sin{\theta} \text{이므로} $$
위에서 설명했듯이 sin^{2} θ+cos^{2} θ=1이므로 sqrt{ 1-cos^{2} θ }=sin θ이다.
$$ \int { { {1} \over {\sqrt{ a^{2}-x^{2} }} } }\, \operatorname{d}\!x = \int { { {1} \over {a \sin{\theta}} } }\, \operatorname{d}\!x = \int { { {1} \over {a \sin{\theta}} } \cdot { {\operatorname{d}\!x} \over {\operatorname{d}\!\theta} } }\, \operatorname{d}\!\theta $$
앞서 나온 식들을 적분에 대입하여 정리한 식이다. 이때, 피적분식을 θ로 정리하였으니 적분변수 또한 θ로 정리해주어야 한다. 여기서 dx/dθ는 적분변수를 θ로 바꾸어주기 위해 사용한 것이다. 여기서 특이한 점이 있다. 일반적으로 치환적분법을 사용할 때에는 피적분식에서 속미분 식을 없애줌과 달리 삼각치환법에서는 피적분식에 속미분식을 집어넣어준다. 즉, 일반적인 치환적분법과 달리 삼각치환법에서는 치환적분법을 역으로 이용한 것이다. 물론 위와 마찬가지로 치환적분법을 이용해 유도하는 것도 가능하나, 본래는 역삼각함수를 배워야 가능한 방법이다.
$$ \int { { {1} \over {a \sin{\theta}} } \cdot { {\operatorname{d}\!x} \over {\operatorname{d}\!\theta} } }\, \operatorname{d}\!\theta = \int { { {1} \over {a \sin{\theta}} } \cdot \left( -a \sin{\theta} \right) }\, \operatorname{d}\!\theta = \int { \left( -1 \right) }\, \operatorname{d}\!\theta $$
앞서 정리한 식에서 dx/dθ에 -a sin θ를 대입하고 정리하면 약분되어 피적분식이 -1이 된다. 즉, 이 부분은 대입하고 식을 정리해주는 과정이다.
$$ \int { \left( -1 \right) }\, \operatorname{d}\!\theta = -\theta+C \left( C \text{는 적분상수} \right) $$
최종적으로 θ에 관한 부정적분 식이 나오게 된다. 이를 다시 x에 관한 식으로 정리하기 위해서는 역삼각함수에 대해 알고 있어야 한다.
$$ \sqrt{ a^{2}-x^{2} } \text{이 포함된 식의 경우 위의 삼각치환법을 사용할 수 있다.} $$
tan, cot 치환
$$ a>0 \text{에 대하여 } x=a\tan{ \theta } \left( -{ {\pi} \over {2} } < \theta < { {\pi} \over {2} } \right) \text{라고 하면} $$
$$ \sqrt{ a^{2}+x^{2} } = a\sec{ \theta } \text{, } { {\operatorname{d}\!x} \over {\operatorname{d}\!\theta} } = a\sec^{2}{\theta} \text{이므로} $$
$$ \int { { {1} \over { a^{2}+x^{2} } } }\, \operatorname{d}\!x = \int { { {1} \over {a} } }\, \operatorname{d}\!\theta $$
$$ a>0 \text{에 대하여 } x=a\cot{ \theta } \left( 0 \le \theta \le \pi \right) \text{라고 하면} $$
$$ \sqrt{ a^{2}+x^{2} } = a\csc{ \theta } \text{, } { {\operatorname{d}\!x} \over {\operatorname{d}\!\theta} } = -a\csc^{2}{\theta} \text{이므로} $$
$$ \int { { {1} \over { a^{2}+x^{2} } } }\, \operatorname{d}\!x = \int { \left( -{ {1} \over {a} } \right) }\, \operatorname{d}\!\theta $$

tan 치환
위에서 밝혔듯이 tan 치환도 예를 통해 알아볼 것이다.
$$ \int { { {1} \over {a^{2}+x^{2}} } }\, \operatorname{d}\!x $$
$$ x = a \tan{\theta} \left( -{ {\pi} \over {2} } < \theta < { {\pi} \over {2} } \right) \text{라고 두면} $$
이와 같이 치환을 하고 θ의 범위를 잡아주는 이유는
1. 1+tan^{2} θ=sec^{2} θ라는 삼각항등식을 이용하기 위해서이다. 이 삼각항등식에 의하여 sqrt{ 1+tan^{2} θ }=sec θ가 된다.
2. tan 함수는 주기함수이며, 일대일함수가 아니므로 치역 내의 어떤 함숫값에 대응하는 정의역 내 원소는 일반적으로 무수히 많다. 그러므로 이와 같이 θ의 범위를 잡아주는 것은 tan 함수를 일대일함수로 만들어주는 효과를 준다.
이다.
$$ \sqrt{ a^{2}+x^{2} } = \sqrt{ a^{2} \left( 1+\tan^{2}{\theta} \right) } = a \sec{\theta} \text{, } { {\operatorname{d}\!x} \over {\operatorname{d}\!\theta} } = a \sec^{2}{\theta} \text{이므로} $$
위에서 설명했듯이 1+tan^{2} θ=sec^{2} θ이므로 sqrt{ 1+tan^{2} θ }=sec θ이다.
$$ \int { { {1} \over {a^{2}+x^{2}} } }\, \operatorname{d}\!x = \int { { {1} \over {a^{2} \sec^{2}{\theta}} } }\, \operatorname{d}\!x = \int { { {1} \over {a^{2} \sec^{2}{\theta}} } \cdot { {\operatorname{d}\!x} \over {\operatorname{d}\!\theta} } }\, \operatorname{d}\!\theta $$
앞서 나온 식들을 적분에 대입하여 정리한 식이다. 이때, 피적분식을 θ로 정리하였으니 적분변수 또한 θ로 정리해주어야 한다. 여기서 dx/dθ는 적분변수를 θ로 바꾸어주기 위해 사용한 것이다. 여기서 특이한 점이 있다. 일반적으로 치환적분법을 사용할 때에는 피적분식에서 속미분 식을 없애줌과 달리 삼각치환법에서는 피적분식에 속미분식을 집어넣어준다. 즉, 일반적인 치환적분법과 달리 삼각치환법에서는 치환적분법을 역으로 이용한 것이다. 물론 위와 마찬가지로 치환적분법을 이용해 유도하는 것도 가능하나, 본래는 역삼각함수를 배워야 가능한 방법이다.
$$ \int { { {1} \over {a^{2} \sec^{2}{\theta}} } \cdot { {\operatorname{d}\!x} \over {\operatorname{d}\!\theta} } }\, \operatorname{d}\!\theta = \int { { {1} \over {a^{2} \sec^{2}{\theta}} } \cdot a \sec^{2}{\theta} }\, \operatorname{d}\!\theta = \int { { {1} \over {a} } }\, \operatorname{d}\!\theta $$
앞서 정리한 식에서 dx/dθ에 a sec^{2} θ를 대입하고 정리하면 약분되어 피적분식이 1/a이 된다. 즉, 이 부분은 대입하고 식을 정리해주는 과정이다.
$$ \int { { {1} \over {a} } }\, \operatorname{d}\!\theta = { {1} \over {a} } \theta+C \left( C \text{는 적분상수} \right) $$
최종적으로 θ에 관한 부정적분 식이 나오게 된다. 이를 다시 x에 관한 식으로 정리하기 위해서는 역삼각함수에 대해 알고 있어야 한다.
cot 치환
위에서 밝혔듯이 cot 치환도 예를 통해 알아볼 것이다.
$$ \int { { {1} \over {a^{2}+x^{2}} } }\, \operatorname{d}\!x $$
$$ x = a \cot{\theta} \left( 0 < \theta < \pi \right) \text{라고 두면} $$
이와 같이 치환을 하고 θ의 범위를 잡아주는 이유는
1. 1+cot^{2} θ=csc^{2} θ라는 삼각항등식을 이용하기 위해서이다. 이 삼각항등식에 의하여 sqrt{ 1+cot^{2} θ }=csc θ가 된다.
2. cot 함수는 주기함수이며, 일대일함수가 아니므로 치역 내의 어떤 함숫값에 대응하는 정의역 내 원소는 일반적으로 무수히 많다. 그러므로 이와 같이 θ의 범위를 잡아주는 것은 cot 함수를 일대일함수로 만들어주는 효과를 준다.
이다.
$$ \sqrt{ a^{2}+x^{2} } = \sqrt{ a^{2} \left( 1+\cot^{2}{\theta} \right) } = a \csc{\theta} \text{, } { {\operatorname{d}\!x} \over {\operatorname{d}\!\theta} } = -a \csc^{2}{\theta} \text{이므로} $$
위에서 설명했듯이 1+cot^{2} θ=csc^{2} θ이므로 sqrt{ 1+cot^{2} θ }=csc θ이다.
$$ \int { { {1} \over {a^{2}+x^{2}} } }\, \operatorname{d}\!x = \int { { {1} \over {a^{2} \csc^{2}{\theta}} } }\, \operatorname{d}\!x = \int { { {1} \over {a^{2} \csc^{2}{\theta}} } \cdot { {\operatorname{d}\!x} \over {\operatorname{d}\!\theta} } }\, \operatorname{d}\!\theta $$
앞서 나온 식들을 적분에 대입하여 정리한 식이다. 이때, 피적분식을 θ로 정리하였으니 적분변수 또한 θ로 정리해주어야 한다. 여기서 dx/dθ는 적분변수를 θ로 바꾸어주기 위해 사용한 것이다. 여기서 특이한 점이 있다. 일반적으로 치환적분법을 사용할 때에는 피적분식에서 속미분 식을 없애줌과 달리 삼각치환법에서는 피적분식에 속미분식을 집어넣어준다. 즉, 일반적인 치환적분법과 달리 삼각치환법에서는 치환적분법을 역으로 이용한 것이다. 물론 위와 마찬가지로 치환적분법을 이용해 유도하는 것도 가능하나, 본래는 역삼각함수를 배워야 가능한 방법이다.
$$ \int { { {1} \over {a^{2} \csc^{2}{\theta}} } \cdot { {\operatorname{d}\!x} \over {\operatorname{d}\!\theta} } }\, \operatorname{d}\!\theta = \int { { {1} \over {a^{2} \csc^{2}{\theta}} } \cdot \left( -a \csc^{2}{\theta} \right) }\, \operatorname{d}\!\theta = \int { \left( -{ {1} \over {a} } \right) }\, \operatorname{d}\!\theta $$
앞서 정리한 식에서 dx/dθ에 -a csc^{2} θ를 대입하고 정리하면 약분되어 피적분식이 -1/a이 된다. 즉, 이 부분은 대입하고 식을 정리해주는 과정이다.
$$ \int { \left( -{ {1} \over {a} } \right) }\, \operatorname{d}\!\theta = -{ {1} \over {a} } \theta+C \left( C \text{는 적분상수} \right) $$
최종적으로 θ에 관한 부정적분 식이 나오게 된다. 이를 다시 x에 관한 식으로 정리하기 위해서는 역삼각함수에 대해 알고 있어야 한다.
$$ \sqrt{ a^{2}+x^{2} } \text{이 포함된 식의 경우 위의 삼각치환법을 사용할 수 있다.} $$
sec, csc 치환
$$ a>0 \text{에 대하여 } x>a \text{, } x=a\sec{ \theta } \left( 0 \le \theta \le \pi \text{, } \theta \ne { {\pi} \over {2} } \right) \text{라고 하면} $$
$$ \sqrt{ x^{2}-a^{2} } = \begin{cases} a \tan{ \theta } & \left( x>a \right) \\ -a \tan{ \theta } & \left( x<-a \right) \end{cases} \text{, } { {\operatorname{d}\!x} \over {\operatorname{d}\!\theta} } = a\sec{\theta} \tan{\theta} \text{이므로} $$
$$ \int { { {1} \over { x \sqrt{ x^{2}-a^{2} } } } }\, \operatorname{d}\!x = \begin{cases} \int { { {1} \over {a} } }\, \operatorname{d}\!\theta & \left( x>a \right) \\ \int { \left( -{ {1} \over {a} } \right) }\, \operatorname{d}\!\theta & \left( x<-a \right) \end{cases} $$
$$ a>0 \text{에 대하여 } x>a \text{, } x=a\csc{ \theta } \left( -{ {\pi} \over {2} } \le \theta \le { {\pi} \over {2} } \text{, } \theta \ne 0 \right) \text{라고 하면} $$
$$ \sqrt{ x^{2}-a^{2} } = \begin{cases} a \cot{ \theta } & \left( x>a \right) \\ -a \cot{ \theta } &
\left( x<-a \right) \end{cases} \text{, } { {\operatorname{d}\!x} \over {\operatorname{d}\!\theta} } = -a \csc{\theta} \cot{\theta} \text{이므로} $$
$$ \int { { {1} \over { x \sqrt{ x^{2}-a^{2} } } } }\, \operatorname{d}\!x = \begin{cases} \int { \left( -{ {1} \over {a} } \right) }\, \operatorname{d}\!\theta & \left( x>a \right) \\ \int { { {1} \over {a} } }\, \operatorname{d}\!\theta & \left( x<-a \right) \end{cases} $$
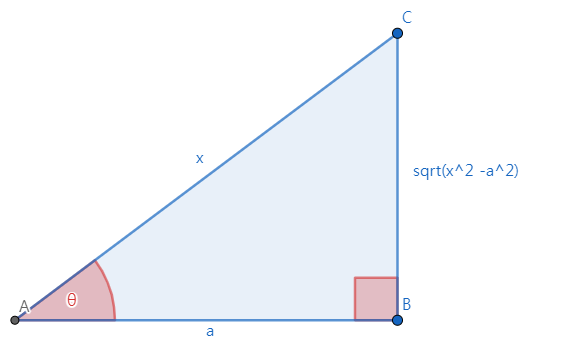
sec 치환
위에서 밝혔듯이 sec 치환도 예를 통해 알아볼 것이다.
$$ \int { { {1} \over {x \sqrt{ x^{2}-a^{2} }} } }\, \operatorname{d}\!x $$
$$ x = a \sec{\theta} \left( x>a \text{, } 0 \le \theta < { {\pi} \over {2} } \right) \text{라고 두면} $$
이와 같이 치환을 하고 θ의 범위를 잡아주는 이유는
1. 1+tan^{2} θ=sec^{2} θ라는 삼각항등식을 이용하기 위해서이다. 이 삼각항등식을 정리하면 sec^{2} θ -1=tan^{2} θ이므로 sqrt{ sec^{2} θ -1 }=tan θ이다.
2. sec 함수는 주기함수이며, 일대일함수가 아니므로 치역 내의 어떤 함숫값에 대응하는 정의역 내 원소는 일반적으로 무수히 많다. 그러므로 이와 같이 θ의 범위를 잡아주는 것은 sec 함수를 일대일함수로 만들어주는 효과를 준다.
이다. 물론 x를 다르게 치환할 수도 있다. x=a sec θ (x<-a, π/2<θ≤π)로도 치환할 수도 있다.
$$ \sqrt{ x^{2}-a^{2} } = \sqrt{ a^{2} \left( \sec^{2}{\theta}-1 \right) } = a \tan{\theta} \text{, } { {\operatorname{d}\!x} \over {\operatorname{d}\!\theta} } = a \sec{\theta} \tan{\theta} \text{이므로} $$
위에서 설명했듯이 1+tan^{2} θ=sec^{2} θ이므로 sqrt{ 1+tan^{2} θ }=sec θ이다. 다르게 치환할 경우4 sqrt{ sec^{2} θ-1 }=-tan θ, dx/dθ = a sec θtan θ가 된다.
$$ \int { { {1} \over {x \sqrt{ x^{2}-a^{2} }} } }\, \operatorname{d}\!x = \int { { {1} \over {a^{2} \sec{\theta} \tan{\theta}} } }\, \operatorname{d}\!x = \int { { {1} \over {a^{2} \sec{\theta} \tan{\theta}} } \cdot { {\operatorname{d}\!x} \over {\operatorname{d}\!\theta} } }\, \operatorname{d}\!\theta $$
앞서 나온 식들을 적분에 대입하여 정리한 식이다. 이때, 피적분식을 θ로 정리하였으니 적분변수 또한 θ로 정리해주어야 한다. 여기서 dx/dθ는 적분변수를 θ로 바꾸어주기 위해 사용한 것이다. 여기서 특이한 점이 있다. 일반적으로 치환적분법을 사용할 때에는 피적분식에서 속미분 식을 없애줌과 달리 삼각치환법에서는 피적분식에 속미분식을 집어넣어준다. 즉, 일반적인 치환적분법과 달리 삼각치환법에서는 치환적분법을 역으로 이용한 것이다. 물론 위와 마찬가지로 치환적분법을 이용해 유도하는 것도 가능하나, 본래는 역삼각함수를 배워야 가능한 방법이다.
$$ \int { { {1} \over {a^{2} \sec{\theta} \tan{\theta}} } \cdot { {\operatorname{d}\!x} \over {\operatorname{d}\!\theta} } }\, \operatorname{d}\!\theta = \int { { {1} \over {a^{2} \sec{\theta} \tan{\theta}} } \cdot a \sec{\theta} \tan{\theta} }\, \operatorname{d}\!\theta = \int { { {1} \over {a} } }\, \operatorname{d}\!\theta $$
앞서 정리한 식에서 dx/dθ에 a sec θtan θ를 대입하고 정리하면 약분되어 피적분식이 1/a이 된다. 즉, 이 부분은 대입하고 식을 정리해주는 과정이다. 다르게 치환할 경우5 피적분식은 -1/a이 된다.
$$ \int { { {1} \over {a} } }\, \operatorname{d}\!\theta = { {1} \over {a} } \theta+C \left( C \text{는 적분상수} \right) $$
최종적으로 θ에 관한 부정적분 식이 나오게 된다. 이를 다시 x에 관한 식으로 정리하기 위해서는 역삼각함수에 대해 알고 있어야 한다. x<-a, π/2 < θ ≤ π인 경우에도 위 방식대로 식을 정리하면 다음과 같은 식이 도출된다.
$$ \int { { {1} \over {x \sqrt{ x^{2}-a^{2} }} } }\, \operatorname{d}\!x = -{ {1} \over {a} } \theta+C \left( C \text{는 적분상수} \right) $$
csc 치환
위에서 밝혔듯이 csc 치환도 예를 통해 알아볼 것이다.
$$ \int { { {1} \over {x \sqrt{ x^{2}-a^{2} }} } }\, \operatorname{d}\!x $$
$$ x = a \csc{\theta} \left( x>a \text{, } 0 \le \theta < { {\pi} \over {2} } \right) \text{라고 두면} $$
이와 같이 치환을 하고 θ의 범위를 잡아주는 이유는
1. 1+cot^{2} θ=csc^{2} θ라는 삼각항등식을 이용하기 위해서이다. 이 삼각항등식을 정리하면 csc^{2} θ -1=cot^{2} θ이므로 sqrt{ csc^{2} θ -1 }=cot θ이다.
2. csc 함수는 주기함수이며, 일대일함수가 아니므로 치역 내의 어떤 함숫값에 대응하는 정의역 내 원소는 일반적으로 무수히 많다. 그러므로 이와 같이 θ의 범위를 잡아주는 것은 csc 함수를 일대일함수로 만들어주는 효과를 준다.
이다. 물론 x를 다르게 치환할 수도 있다. x=a csc θ (x<-a, -π/2≤θ<0)로도 치환할 수도 있다.
$$ \sqrt{ x^{2}-a^{2} } = \sqrt{ a^{2} \left( \csc^{2}{\theta}-1 \right) } = a \cot{\theta} \text{, } { {\operatorname{d}\!x} \over {\operatorname{d}\!\theta} } = -a \csc{\theta} \cot{\theta} \text{이므로} $$
위에서 설명했듯이 1+cot^{2} θ=csc^{2} θ이므로 sqrt{ csc^{2} θ-1 }=cot θ이다. 다르게 치환할 경우6 sqrt{ csc^{2} θ-1 }=-cot θ, dx/dθ = -a csc θcot θ가 된다.
$$ \int { { {1} \over {x \sqrt{ x^{2}-a^{2} }} } }\, \operatorname{d}\!x = \int { { {1} \over {a^{2} \csc{\theta} \cot{\theta}} } }\, \operatorname{d}\!x = \int { { {1} \over {a^{2} \csc{\theta} \cot{\theta}} } \cdot { {\operatorname{d}\!x} \over {\operatorname{d}\!\theta} } }\, \operatorname{d}\!\theta $$
앞서 나온 식들을 적분에 대입하여 정리한 식이다. 이때, 피적분식을 θ로 정리하였으니 적분변수 또한 θ로 정리해주어야 한다. 여기서 dx/dθ는 적분변수를 θ로 바꾸어주기 위해 사용한 것이다. 여기서 특이한 점이 있다. 일반적으로 치환적분법을 사용할 때에는 피적분식에서 속미분 식을 없애줌과 달리 삼각치환법에서는 피적분식에 속미분식을 집어넣어준다. 즉, 일반적인 치환적분법과 달리 삼각치환법에서는 치환적분법을 역으로 이용한 것이다. 물론 위와 마찬가지로 치환적분법을 이용해 유도하는 것도 가능하나, 본래는 역삼각함수를 배워야 가능한 방법이다.
$$ \int { { {1} \over {a^{2} \csc{\theta} \cot{\theta}} } \cdot { {\operatorname{d}\!x} \over {\operatorname{d}\!\theta} } }\, \operatorname{d}\!\theta = \int { { {1} \over {a^{2} \csc{\theta} \cot{\theta}} } \cdot \left( -a \csc{\theta} \cot{\theta} \right) }\, \operatorname{d}\!\theta = \int { \left( -{ {1} \over {a} } \right) }\, \operatorname{d}\!\theta $$
앞서 정리한 식에서 dx/dθ에 -a csc θcot θ를 대입하고 정리하면 약분되어 피적분식이 -1/a이 된다. 즉, 이 부분은 대입하고 식을 정리해주는 과정이다. 다르게 치환할 경우7 피적분식은 1/a이 된다.
$$ \int { \left( -{ {1} \over {a} } \right) }\, \operatorname{d}\!\theta = -{ {1} \over {a} } \theta+C \left( C \text{는 적분상수} \right) $$
최종적으로 θ에 관한 부정적분 식이 나오게 된다. 이를 다시 x에 관한 식으로 정리하기 위해서는 역삼각함수에 대해 알고 있어야 한다. x<-a, π/2 < θ ≤ π인 경우에도 위 방식대로 식을 정리하면 다음과 같은 식이 도출된다.
$$ \int { { {1} \over {x \sqrt{ x^{2}-a^{2} }} } }\, \operatorname{d}\!x = { {1} \over {a} } \theta+C \left( C \text{는 적분상수} \right) $$
$$ \sqrt{ x^{2}-a^{2} } \text{이 포함된 식의 경우 위의 삼각치환법을 사용할 수 있다.} $$
정리
위에서 볼 수 있듯이 삼각치환법은 치환적분법을 역으로 이용한 결과8이다. 위 6가지 삼각치환법을 다음의 표와 같이 정리할 수 있다. 위 6가지 삼각치환법은 적분하는 식에 포함된 식의 형태에 따라 크게 3가지로 나눌 수 있으므로 식의 형태별로 3가지 방법만 알고 있어도 문제를 푸는데 지장이 없다.
| 순번 | 적분에 포함된 식 | 치환 | 범위 | |
| ① | $$ \sqrt{ a^{2}-x^{2} } $$ | $$ x = a \sin{\theta} $$ | $$ -{ {\pi} \over {2} } \le \theta \le { {\pi} \over {2} } $$ | $$ \sqrt{ a^{2}-x^{2} } = a \cos{\theta} $$ |
| ② | $$ x = a \cos{\theta} $$ | $$ 0 \le \theta \le \pi $$ | $$ \sqrt{ a^{2}-x^{2} } = a \sin{\theta} $$ | |
| ③ | $$ \sqrt{ a^{2}+x^{2} } $$ | $$ x = a \tan{\theta} $$ | $$ -{ {\pi} \over {2} } \le \theta \le { {\pi} \over {2} } $$ | $$ \sqrt{ a^{2}+x^{2} } = a \sec{\theta} $$ |
| ④ | $$ x = a \cot{\theta} $$ | $$ 0 \le \theta \le \pi $$ | $$ \sqrt{ a^{2}+x^{2} } = a \sec{\theta} $$ | |
| ⑤ | $$ \sqrt{ x^{2}-a^{2} } $$ | $$ x = a \sec{\theta} $$ | >$$ 0 \le \theta \le \pi \text{, } \theta \ne { {\pi} \over {2} } $$ | $$ \sqrt{ x^{2}-a^{2} } = \begin{cases} a \tan{\theta} & \left( x>a \text{, } 0 \le \theta < { {\pi} \over {2} } \right) \\ -a \tan{\theta} & \left( x<-a \text{, } { {\pi} \over {2} } < \theta \le \pi \right) \end{cases} $$ |
| ⑥ | $$ x = a \csc{\theta} $$ | $$ -{ {\pi} \over {2} } \le \theta \le { {\pi} \over {2} } \text{, } \theta \ne 0 $$ | $$ \sqrt{ x^{2}-a^{2} } = \begin{cases} a \cot{\theta} & \left( x>a \text{, } 0 \le \theta < { {\pi} \over {2} } \right) \\ -a \cot{\theta} & \left( x<-a \text{, } -{ {\pi} \over {2} } < \theta \le 0 \right) \end{cases} $$ |
| 순번 | 사용된 삼각함수의 성질 | |
| ① | $$ { {\operatorname{d}\!x} \over {\operatorname{d}\!\theta} } = a \cos{\theta} $$ | $$ \sin^{2}{\theta} + \cos^{2}{\theta} = 1 $$ |
| ② | $$ { {\operatorname{d}\!x} \over {\operatorname{d}\!\theta} } = -a \sin{\theta} $$ | $$ 1+\tan^{2}{\theta} = \sec^{2}{\theta} $$ |
| ③ | $$ { {\operatorname{d}\!x} \over {\operatorname{d}\!\theta} } = a \sec^{2}{\theta} $$ | $$ 1+\tan^{2}{\theta} = \sec^{2}{\theta} $$ |
| ④ | $$ { {\operatorname{d}\!x} \over {\operatorname{d}\!\theta} } = -a \csc^{2}{\theta} $$ | $$ 1+\cot^{2}{\theta} = \csc^{2}{\theta} $$ |
| ⑤ | $$ { {\operatorname{d}\!x} \over {\operatorname{d}\!\theta} } = a \sec{\theta} \tan{\theta} $$ | $$ 1+\tan^{2}{\theta} = \sec^{2}{\theta} $$ |
| ⑥ | $$ { {\operatorname{d}\!x} \over {\operatorname{d}\!\theta} } = -a \csc{\theta} \cot{\theta} $$ | $$ 1+\cot^{2}{\theta} = \csc^{2}{\theta} $$ |
신은 솜씨 좋은 기하학자와 같다.
-토마스 브라운
'수학 > 고등학생을 위한 수학' 카테고리의 다른 글
| 미분과 적분(43) (0) | 2021.01.06 |
|---|---|
| 미분과 적분(42) (0) | 2021.01.05 |
| 미분과 적분(40) (0) | 2021.01.01 |
| 삼각함수(1) (0) | 2020.12.28 |
| 미분과 적분(39) (0) | 2020.12.21 |

