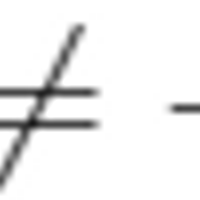미분과 적분(28)

※본 글에는 수식이 사용되었습니다. 모바일에서는 수식이 깨져 보이지 않을 수 있는 점 참고 바랍니다. 만일 수식이 깨져 보일 경우 데스크톱 모드를 사용하여 주시길 부탁드립니다.

---

 앞에서 미분에 대해 알아보았다. 이번 글에서부터는 적분에 대하여 다룰 것이다. 먼저 우리나라에서 미적분을 배우는 과정을 살펴보자. 아래의 표는 큰 주제만 따와 구성한 우리나라의 미적분 교육과정이다. 표 상단에 위치할수록 더 먼저 배운다.

극한
미분		부정적분
적분		정적분

이 표를 보면 알 수 있듯이 극한을 배운 미분을 배우고, 이후 적분을 배운다. 그러나 수학사적으로는 적분이 가장 먼저 만들어졌고, 또한 가장 먼저 사용되어 왔다. 뿐만 아니라 부정적분보다도 정적분이 더 먼저 사용되어 왔다. 그렇다면 우리는 왜 적분을 미분보다 먼저 배우지 않고, 왜 정적분을 부정적분보다 먼저 배우지 않을까? 이유는 간단하다. 이러한 순서로 배우는 것이 개념을 이해하기 좋고, 미적분학의 기본원리를 이용할 수 있어 계산하는데 편하기 때문이다. 그러므로 여기서도 교육과정의 순서에 따라 부정적분을 먼저 다룰 것이다.

 먼저 새로운 개념을 정리해 보자. 부정적분은 다음과 같이 정의한다.

두 함수 F(x), f(x)에 대하여 다음을 만족하는 함수 F(x)를 함수 f(x)의 부정적분이라 한다.
$$ F^{\prime}(x) = f(x) $$

이 정의에 의하여 어떤 함수의 부정적분인 함수는 무수히 많다.^[각주:1] 이러한 까닭에 정해지지 않다라는 뜻의 '부정'이라는 단어를 사용하여 부정적분이라고 이름을 붙인 것이다. 이로 인해 어떤 함수든 부정적분을 구하면 미분을 하면서 사라진 상수를 복구시켜야 하는데, 이때 상수값을 알지 못하므로 미지수로 둔다. 이 미지수를 적분상수라 하고 주로 C로 표현한다.

예시

$$ F^{\prime}(x) = f(x) \text{인 두 함수 } F(x), f(x) \text{에 대하여 } F(x) = \int {f(x)}\, \operatorname{d}\!x +C \left( C \text{는 적분상수} \right) $$

여기서 기호 ∫은 적분을 표현하는 기호로 인테그랄(integral)이라고 하며, ∫f(x) dx는 함수 f(x)를 x에 대하여 적분하라는 뜻이다.^[각주:2]

 부정적분의 정의에서 알 수 있는 사실이 한 가지 더 있다. 부정적분을 구하는 것은 '미분의 역연산'이라는 점이다. 이 점은 딱히 중요해 보이지 않을 수 있다. 그러나 후에 다룰 적분 공식들은 모두 이러한 특징에서 도출이 된다. 뿐만 아니라 어떤 함수 f(x)의 부정적분을 구해야 해결할 수 있는 문제를 풀 때 미분해서 함수 f(x)가 나오는 함수 g(x)가 갑자기 생각난다면, 위 성질에 의하여 함수 g(x)에 적분상수 C를 더한 함수 g(x)+C가 바로 함수 f(x)의 부정적분이 되므로 좀 더 빠르게 부정적분을 구할 수 있다.^[각주:3]

 이전에 미분 파트에서 미분 공식을 다루었듯이 적분에서도 마찬가지로 적분 공식을 다룰 것이다. 다음은 n차 다항함수의 부정적분에 대해 다룰 것이다.

 

 

 

수학의 앞날을 내다보는 참된 방법은 그 역사와 현재의 상태를 살펴보는 것이다.

-푸앵카레

---

1. 상수 a를 x에 대하여 미분하면 0이다. [본문으로]
2. 즉, 변수를 x로 둔다는 뜻이다. 이 점을 주의하지 않으면 전혀 다른 식을 도출해낼 수 있다. [본문으로]
3. 이것이 익숙해지면 문제를 푸는데 걸리는 시간과 풀이과정을 단축할 수 있다. 그러나 익숙하지 않음에도 불구하고 억지로 찾아내려는 통칭 '노가다'라고 부르는 것을 하기 시작하면 필연적으로 풀이 시간은 더 오래 걸릴 것이다. [본문으로]