※본 글에는 수식이 사용되었습니다. 모바일에서는 수식이 깨져 보이지 않을 수 있는 점 참고 바랍니다. 만일 수식이 깨져 보일 경우 데스크톱 모드를 사용하여 주시길 부탁드립니다.
좌표평면 상에 무작위로 흩어져 있는 벡터는 연산을 하거나 평행 여부를 판단하기 어렵다. 이때, 두 벡터의 크기와 방향이 같으면 위치에 관계없이 두 벡터는 같다. 그러므로 우리는 편의를 위해 좌표평면 상에서 시점을 (0, 0)으로 하는 벡터를 주로 사용할 것이다. 이렇게 원점을 시점으로 하는 벡터를 '위치벡터'라고 한다.
위치벡터의 성분
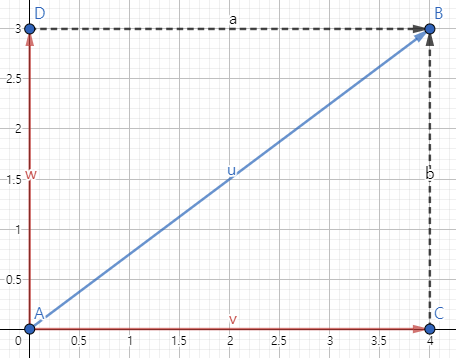
위치벡터의 표현은 주로 좌표를 이용해 (a, b)와 같이 나타낸다. 위의 그림을 보면 두 위치벡터 (4, 0)과 (0, 3)을 더하면 위치벡터 (4, 3)이 나옴을 알 수 있다. 이때, 두 위치벡터 (4, 0)과 (0, 3)은 각각 x축과 y축에 평행한 벡터이다. 이처럼 x축에 평행한 벡터와 y축에 평행한 벡터를 합성하여 위치벡터 (a, b)가 나오도록 하는 두 벡터는 (a, 0), (0, b)의 꼴로 항상 존재한다.1 즉, 두 위치벡터 (a, 0), (0, b)는 각각 x축, y축에 평행하며, 두 벡터를 합성하면 위치벡터 (a, b)가 나오므로 a를 위치벡터 (a, b)의 x성분, b를 위치벡터 (a, b)의 y성분이라고 한다.
단위벡터
단위벡터는 길이가 1인 벡터로 정의한다. 그러므로 위치벡터 (a, b)에 대하여 a^{2}+b^{2}=1을 만족하면 이 위치벡터는 단위벡터이다. 그 중 x성분 또는 y성분이 0인 단위벡터는 (1, 0), (0, 1)로 두 개가 있다. 이렇게 위치벡터 중 (1, 0), (0, 1)을 기본단위벡터라고 하며, 주로 다음과 같이 표현한다.
$$ (1 \text{, } 0) = e_{1} \text{, } (0 \text{, } 1) = e_{2} $$
나에게는 수학이 만물으로 환원된다.
-데카르트
- 단, a≠0, b≠0 [본문으로]
'수학 > 고등학생을 위한 수학' 카테고리의 다른 글
| 기하와 벡터(20) (0) | 2021.02.21 |
|---|---|
| 확률과 통계(1) (0) | 2021.02.19 |
| 기하와 벡터(18) (0) | 2021.02.11 |
| 기하와 벡터(17) (0) | 2021.02.08 |
| 기하와 벡터(16) (0) | 2021.02.07 |


