새창으로 열기 - [목차] 중학교 대수 - 중학생을 위한 수학
※본문에는 수식이 사용되었습니다. 모바일에서는 수식이 깨져 보이지 않을 수 있는 점 참고 바랍니다. 만일 수식이 깨져 보일 경우 데스크톱 모드를 사용하여 주시길 부탁드립니다.
우리는 편의를 위해 명확한 기준을 통해 수많은 개념을 구분하고, 이를 바탕으로 각 개념을 확장해 나간다. 분수를 가분수와 진분수로, 다각형을 삼각형과 사각형, 오각형 등으로 구분하듯이 자연수 또한 홀수와 짝수로 구분할 수 있다. 이러한 자연수는 약수의 개수에 따라 구분할 수도 있으며, 본문에서는 이에 대하여 다루고자 한다.
1과 소수와 합성수
자연수를 짝수와 홀수로 구분하는 방법은 각 자연수가 2의 배수인지 아닌지1로 판단하여 구분한다. 이와 마찬가지로 자연수를 구분하는 또 다른 방법이 있는데, 이 방법이 약수의 개수에 따라 구분하는 방법이다. 모든 자연수는 자기 자신을 포함하여 다른 자연수들의 곱으로 표현할 수 있는데, 이러한 표현에 사용할 수 있는 모든 자연수를 그 자연수의 약수라고 한다. 예를 들어 1의 약수는 1, 2의 약수는 1, 2, 4의 약수는 1, 2, 4가 된다. 자연수의 약수를 구하다 보면 1과 자기 자신만을 약수로 가지는, 다시 말해 약수의 개수가 2개뿐인 자연수를 심심찮게 볼 수 있다. 이처럼 성질을 가지는 자연수를 소수라고 한다. 이와 달리 1과 자기 자신을 제외하고 다른 약수를 가지는, 즉 약수의 개수가 3개 이상인 자연수를 합성수라고 한다. 그렇다면 무수히 많은 자연수 중에 이러한 특징을 가지는 소수를 어떻게 골라낼 수 있을까?
소수를 찾는 방법
소수는 1과 자기자신만을 약수로 가지므로 소수의 배수는 모두 합성수가 된다. 즉, 소수 하나를 찾을 때마다 그 소수의 배수를 모두 지우는 작업을 반복하면 소수만이 남을 것으로 기대할 수 있다. 그러므로 다음 과정을 통해 주어진 범위에서의 소수를 찾아낼 수 있다.
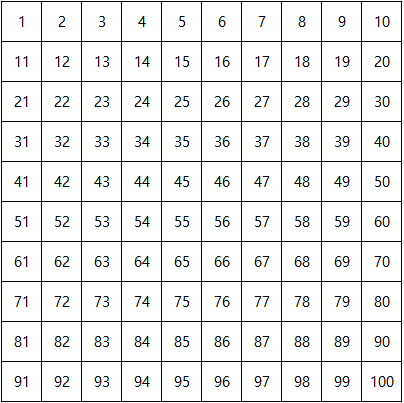
- 1은 소수가 아니므로 지운다.2
- 남은 수 중 가장 작은 수인 2를 살린다.
- 2를 제외한 2의 배수는 모두 합성수이므로 2를 제외한 모든 2의 배수를 지운다.
- 남은 수 중 가장 작은 수인 3을 살린다.
- 3을 제외한 3의 배수는 모두 합성수이므로 3을 제외한 모든 3의 배수를 지운다.
- 남은 수 중 가장 작은 수인 5를 살린다.
- 5를 제외한 5의 배수는 모두 합성수이므로 5를 제외한 모든 5의 배수를 지운다.
- 남은 수 중 가장 작은 수를 살리고, 그 수를 제외한 그 수의 배수를 모두 지우는 과정을 반복한다.
에라토스테네스의 체
100 이하의 모든 소수를 에라토스테네스의 체를 이용해 구해보자. 먼저 1은 소수가 아니므로 지운다.
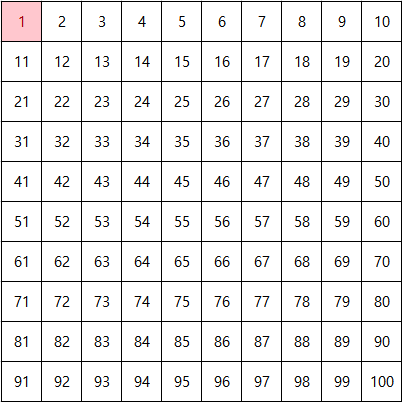
남은 수 중 가장 작은 수인 2를 살리고, 그 외에 2의 배수는 지운다.
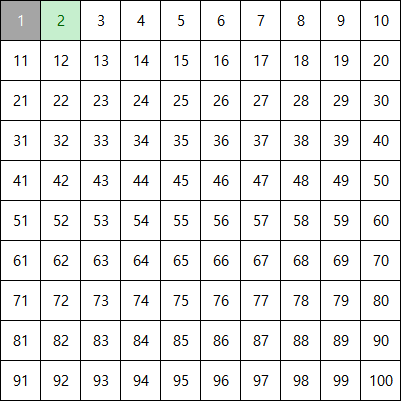
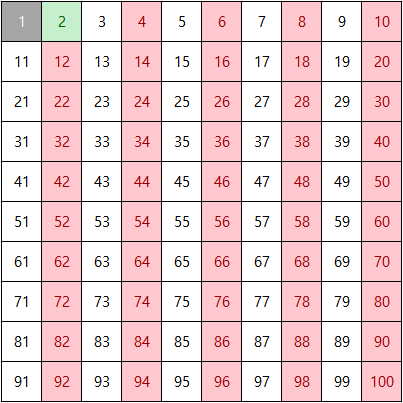
남은 수 중 가장 작은 수인 3을 살리고, 그 외에 3의 배수는 지운다.
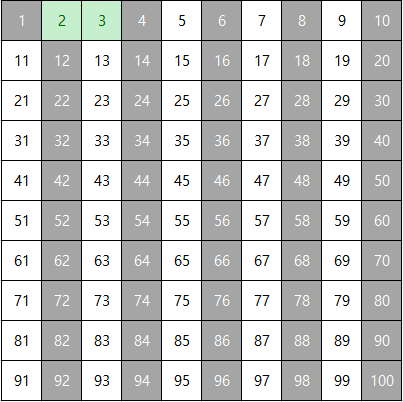
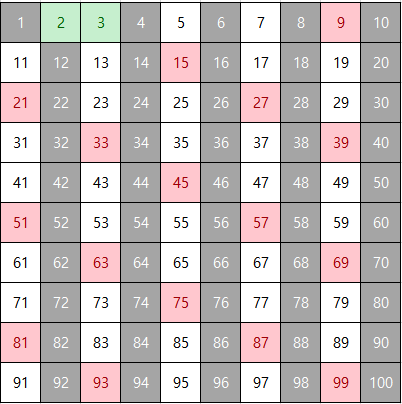
남은 수 중 가장 작은 수인 5를 살리고, 그 외에 5의 배수는 지운다.
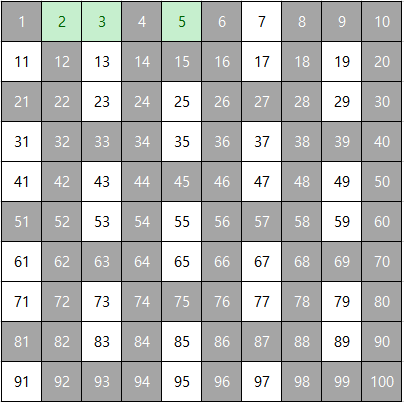
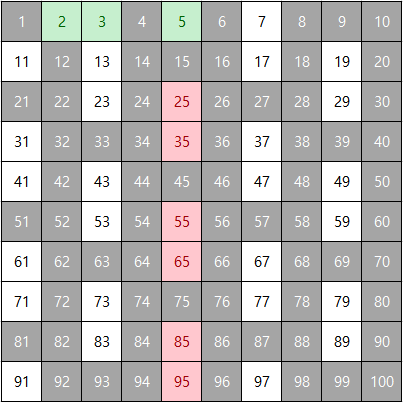
남은 수 중 가장 작은 수인 7을 살리고, 그 외에 7의 배수는 지운다.
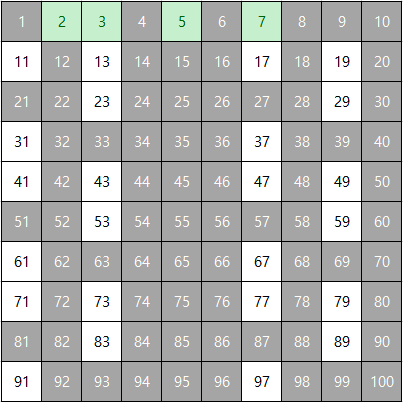
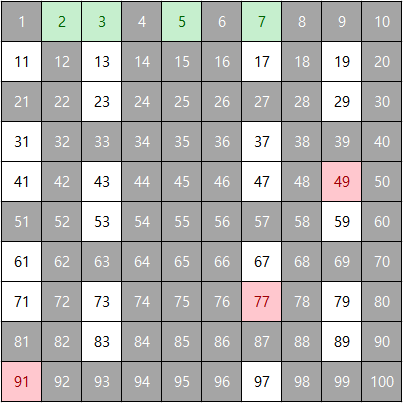
위와 같이 남은 수 중 가장 작은 수를 살리고, 그 수의 배수를 지우는 과정을 반복한다.
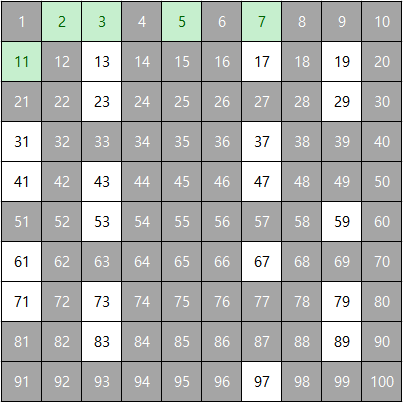
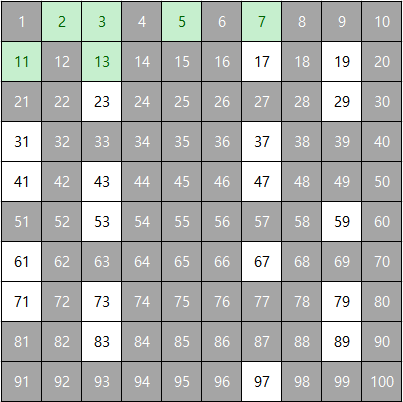
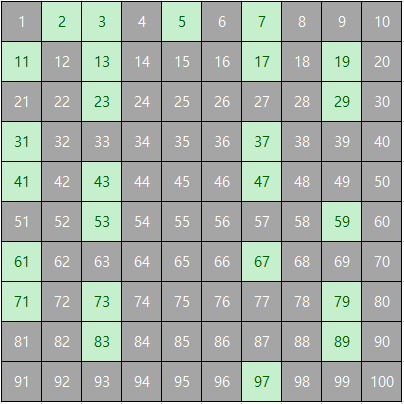
따라서 100 이하의 소수는 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97로 총 25개가 있다.
이러한 과정을 따라가면 2, 3, 5, 7, 11, \( \cdots \)과 같은 소수만이 남게 된다. 이러한 과정을 통해 소수를 찾는 방법은 고대 그리스의 수학자 에라토스테네스가 고안한 것으로 마치 크기가 다른 알갱이를 '체'를 이용해 골라내듯이 소수를 골라내는 것 같다고 하여 <에라토스테네스의 체>라고 불린다.
수학의 어떤 두 분야도 산술학과 정수론만큼 대조적이지 않다.
-토비아스 단치히
'수학 > 중학생을 위한 수학' 카테고리의 다른 글
| [서론] 중학생을 위한 수학 (0) | 2021.07.10 |
|---|