※본문에는 수식이 사용되었습니다. 모바일에서는 수식이 깨져 보이지 않을 수 있는 점 참고 바랍니다. 만일 수식이 깨져 보일 경우 데스크톱 모드를 사용하여 주시길 부탁드립니다.
새창으로 열기 - [목차] 화학 II - 고등학생을 위한 과학
주사기의 구멍을 막고 힘을 가해주거나 공기가 차있는 풍선에 힘을 가해주면 주사기와 풍선이 차지하는 부피는 감소한다. 이는 외부압력을 가해주었을 때, 기체의 부피가 감소한다는 뜻과도 같다. 그렇다면 압력과 부피는 어떠한 관계를 가지고 있다는 뜻이 된다. 본문에서는 기체의 압력과 부피 사이의 관계를 설명하는 보일 법칙에 대해 알아볼 것이다.
보일 법칙
보일법칙은 온도가 일정할 때, 일정량의 기체의 부피(\( V \))와 압력(\( P \))은 반비례 관계에 있음을 말하는 법칙이다. 어떻게 이런 일이 가능할까? 아래 그림과 같이 기체가 들어있는 피스톤을 장치하고, 일정한 온도에서 외부 압력을 2배, 3배로 증가시키면 기체의 기체의 부피가 \( \frac{1}{2} \)배, \( \frac{1}{3} \)배로 감소한다.
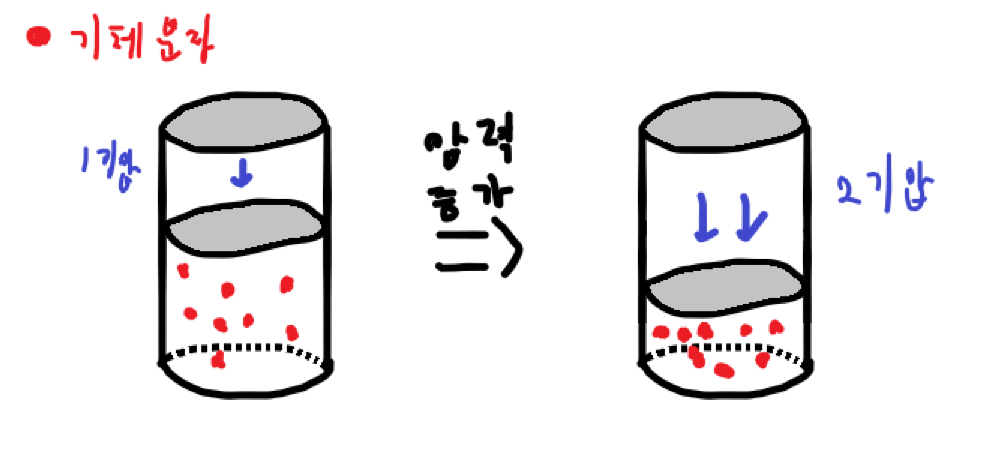
따라서 단위 부피당 분자 수가 2배, 3배로 증가하게 되고, 이는 곧 단위 면적당 충돌 횟수도 2배, 3배로 증가하는 결과를 낳는다. 충돌횟수가 증가하면 이에 비례하여 단위 면적에 미치는 힘의 크기, 즉 기체의 압력 또한 같이 증가하므로 기체의 압력이 2배, 3배로 증가하게 된다. 그러므로 기체의 부피와 압력은 반비례 관계에 있고,
$$ V \propto \frac{1}{P} $$
온도가 일정할 때, 일정량의 기체의 압력과 부피의 곱은 항상 일정하다고 할 수 있다.
\( PV = k \) (단, \( k \)는 상수)
보일 법칙의 그래프
아래의 그림은 모두 보일 법칙을 나타내는 그래프이다. 그래프의 조건은 모두 기체의 양(\( \mathrm{mol} \))과 온도(\( T \))로 일정하다.
부피(\( V \))-압력(\( P \)) 그래프

기체의 부피는 압력에 반비례하므로 \( V \)-\( P \) 그래프는 쌍곡선의 일부를 그래프로 가진다.
\( PV \)-\( P \)(또는 \( V \)) 그래프

기체의 부피와 압력의 곱은 항상 일정하므로 \( PV \)-\( P \)(또는 \( V \)) 그래프는 \( PV \)축에 수직인 직선을 그래프로 가진다.
\( \frac{1}{V} \)-\( P \) 그래프

기체의 부피는 압력에 반비례하므로 \( \frac{1}{V} \)-\( P \) 그래프는 정비례 그래프, 즉 원점을 지나는 직선의 형태로 표현된다.
내게 천 가지의 아이디어가 있고, 그중 하나가 쓸모가 있다면 나는 그것으로 만족한다.
-노벨

